|
Календарь мероприятий
апрель  2024
Пн |
Вт |
Ср |
Чт |
Пт |
Сб |
Вс |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | | | | | |
показать все 
Новости партнеров
Ассоциация разработчиков «Отечественный софт» отметила 15-летие
Читать далее
РДТЕХ представил Технологическую карту российского ПО 2023
Читать далее
RAMAX Group получила партнерский статус уровня Gold по продукту Tarantool
Читать далее
На RIGF 2024 обсудили ключевые вопросы цифрового развития России
Читать далее
показать все
Статьи
5 способов повысить безопасность электронной подписи
Читать далее
Как искусственный интеллект изменит экономику
Читать далее
Неочевидный САПР: выход ПО за рамки конструкторской деятельности
Читать далее
Скоро некому будет делать сайты и заниматься версткой
Читать далее
Цифровая трансформация в энергетике: как запустить проект с максимальным финансовым эффектом?
Читать далее
Мотивируй, не то проиграешь!
Читать далее
В 2024 году в России и мире вырастут объемы применения AR/VR
Читать далее
Цифровые технологии: надежды и риски
Читать далее
Будут ли востребованы услуги технической поддержки софта Oracle в России в ближайшие годы?
Читать далее
Здания с признаками интеллекта. Как Сергей Провалихин автоматизирует дома и производства
Читать далее
показать все
|
Проанализируй принятые решения и оцени их точность
Главная /
Архив номеров / 2016 / Выпуск №10 (63) / Проанализируй принятые решения и оцени их точность
Рубрика:
ИТ-управление
Facebook
Мой мир
Вконтакте
Одноклассники
Google+
Эдуард Клышинский, к.т.н., доцент департамента компьютерной инженерии НИУ ВШЭ
Проанализируй принятые решения
и оцени их точность
 Есть несколько базовых принципов, владение которыми помогает повысить обоснованность принимаемых решений. Как и героев фильма «Девять дней одного года», при принятии решений нас может поджидать как успех, так и неудача. Но если, как и герои упомянутого фильма, мы стремимся кистине, то должны понимать, корректна ли наша стратегия принятия решений или нет
Как известно, точность – вежливость королей. Кроме того, под точностью понимается количественный показатель, показывающий, насколько правильно мы принимаем решения. Давайте на одном частном примере разберем методику численной оценки точности принимаемых решений.
Представим себе, что в течение последнего времени мы многократно принимали решения в некоторой стандартной ситуации, например стоит ли выдавать кредиты приходящим клиентам. В ходе принятия решения мы рассматривали один из трех исходов: выдать, отказать и уклониться от принятия решения (отправить бумаги к более опытному менеджеру). По истечении некоторого времени мы получили информацию по каждому принятому решению – было оно правильным или нет.
Для каждого клиента с кредитом, выданным в нашем банке, это информация о его погашении. Для клиента с отказом мы можем получить информацию из межбанковской системы, куда все банки должны направлять информацию о кредитных историях (давайте считать, что рано или поздно, но клиент найдет банк, который выдаст ему кредит).
Теперь всех клиентов, по которым мы принимали решение, можно разделить на четыре группы: очень хорошо, что выдали (нет просрочек); зря выдали (есть просрочки); хорошо, чтоне выдали (есть просрочки в чужом банке); зря не выдали (нет просрочек в чужом банке). Всякий раз, когда мы зря выдавали или не выдавали кредит, мы ошибались и теряли клиентов или деньги. Обладая итоговой статистикой, мы можем оценить, насколько хорошо мы работаем. Для этого можно посчитать точность – отношение числа случаев, когда мыпринимали решение корректно, к общему количеству рассматриваемых случаев.
Поясним на цифрах. Пусть к нам пришли 110 клиентов, и для 100 из них мы приняли решение самостоятельно. Мы решили выдать 60 кредитов, а 40 клиентам отказали.
Через год мы выяснили, что успешно возвращали кредит 50 наших клиентов (хорошо, что выдали – истинно положительное решение) и 10 клиентов чужого банка (зря не выдали – ложно отрицательное решение). Не возвращали кредиты 10 наших клиентов (зря выдали – ложно положительное решение) и 30 клиентов чужого банка (хорошо, что не выдали – истинно отрицательное решение).
Таким образом, мы приняли 50 + 30 = 80 правильных решений из 110, то есть точность нашего алгоритма принятия решений составляет 8/11.
Если у вас есть несколько сотрудников, принимающих подобные решения, можно количественно оценить точность работы каждого из них. Например, путем корректировки зарплаты.
Однако после первых изменений неуспешные сотрудники попытаются минимизировать свои издержки. Например, это достигается за счет перехода в режим отказа от принятия решения в сложном случае: если менеджер видит, что принимаемое решение является очевидным и правильным, то он будет его принимать, в противном случае он отправит клиента наверх. Подобная стратегия поведения повысит точность принимаемых решений, но существенно увеличит нагрузку на менеджера более высокого уровня.
В ответ мы можем начать считать еще один показатель – полноту, которая определяется как число принятых решений к общему количеству объектов, для которых оно должно было быть принято. Так, для предыдущего примера полнота принятия решений составит 10/11.
Вернемся к нашим клиентам. Пусть для следующего периода (следующие 110 клиентов, новая стратегия поведения менеджеров) статистика принятия решений распределилась следующим образом: 30 истинно положительных решений, 5 ложно положительных, 20 истинно отрицательных решений, 5 ложно отрицательных, 50 раз дело отправлялось наверх (отказ от принятия решения).
Итого: полнота принятия решений составила (30 + 5 + 20 + 5)/110 = 6/11, а точность принятия решений равна (30 + 20)/110 = 5/11. Итак, мало того, что точность принятия решения упала, так теперь решения принимает менеджер с более высокой зарплатой.
Очевидно, что нас такое решение не устраивает, и мы переводим менеджеров на сдельную оплату по числу принятых решений, причем штрафуем за каждое непринятое решение.
В ответ менеджеры разделяются на два лагеря: первые предвкушают грядущие беды и подают заявление об увольнении, вторые повышают полноту до единицы, при этом у них падает точность (пусть они ошибаются во всех спорных случаях, то есть точность будет равна 0,73). А что, за «плохих» клиентов мы же их не штрафуем!
Теперь мы понимаем, что должен быть какой-то баланс между полнотой и точностью. Нам нужна какая-то оценка, которая учитывала бы и то, и другое. Наняв аналитика, мывыясняем, что такая оценка есть, и называется она F-мера. F-мера определяется как отношение произведения точности и полноты к их сумме. Обычно ее умножают на 2, чтобы работать с интервалом от 0 до 1, и говорят о F1-мере. Делать это не обязательно, и дальше мы этого делать не будем (то есть все значения F-меры у нас будут меняться от 0 до 0,5).
Используя F-меру, мы понимаем, что в первом случае она равнялась 0,4; для второго – 0,25; для третьего – 0,42. Как мы видим, надо было с самого начала вводить в качестве KPI именно F-меру, а не отдельные ее составляющие. Итоговая стратегия работает несколько лучше.
По ходу работы с аналитиком к нам приходит понимание, что, принимая решение о выдаче кредитов, мы решаем задачу классификации клиентов. У нас уже имеется натренированный классификатор (менеджер), и он классифицирует всех клиентов на три класса: выдать кредит, не выдавать кредит, сомнительный случай. Это уже знакомая нам задача, к которой можно применить методы машинного обучения.
Кстати, заодно мы можем попробовать несколько разных методов и выбрать тот, который на нашей истории дает результаты получше. Только надо иметь в виду, что классификатор может натренироваться именно на нашу историю и будет давать сбой на новых данных. Поэтому обучать лучше на одних данных, а тестировать на других.
Например, мы можем выбрать 80% имеющейся информации для обучения, а оставшиеся 20% использовать для тестирования. Если мы проведем такую операцию несколько раз, выделяя для тестирования разные фрагменты, а классификатор каждый раз будет выдавать результат со сходной точностью, значит, метод должен быть и в самом деле хорош.
Итак, мы зовем нашего аналитика, даем ему программиста, и они создают нам программу для автоматизации принятия решений о выдаче кредитов. Далее мы проводим реинжиниринг бизнес-процессов, оптимизируем затраты на менеджеров и существенно повышаем эффективность работы отдельного менеджера нижнего звена. После чего понимаем, что почивать на лаврах рановато, так как нам хочется достигнуть большего. Нельзя ли так настроить систему, чтобы она обладала F-мерой, равной единице?
У нас имеется модель принятия решений. Данная модель обладает какими-то параметрами, которые определяют процент отказов клиентам. Представим себе две крайние ситуации. В первом случае мы выставим на модели параноидальный режим, то есть система будет отказывать всем приходящим клиентам. Получится, что мы откажем всем «плохим» клиентам, но лишимся и всех «хороших», то есть полнота работы системы будет низкой.
Хорошо, во втором случае мы выставим параметры модели так, чтобы она всегда соглашалась. Тогда мы будем работать как со всеми «хорошими», так и со всеми «плохими» клиентами, полнота равна единице. Но в этом случае точность работы системы принятия решений будет зависеть от соотношения количества «плохих» и «хороших» клиентов, которые приходят в наш банк.
Интуитивно мы понимаем, что где-то посредине находятся значения параметров модели, позволяющие выдавать кредиты всем «хорошим» клиентам, а всем «плохим» отказывать.
Мы продолжаем анализировать ситуацию и приходим к следующей неожиданной идее. А давайте посмотрим отдельно на точность по каждому из классов. Для принятия решения имеется три класса, два из которых характеризируют наших клиентов. В такой ситуации удобнее считать, что клиенты тоже могут быть отнесены к трем классам, просто на самом деле ни один клиент не принадлежит классу «отложить решение».
Теперь мы можем построить квадратную матрицу, по строкам которой идут истинные классы клиентов, а по столбцам – принятое нами решение. Используя эту матрицу, мы можем посчитать точность и полноту не только для решения в целом, но и для каждого класса в отдельности (с точки зрения теории это будет правильным решением, в отличие отпредыдущего). Точность теперь будет считаться для принятых решений, а полнота – для истинных классов клиентов. То есть точность для класса будет считаться как количество объектов (клиентов), правильно отнесенных к данному классу (элемент на диагонали), к общему количеству объектов, для которых мы приняли такое решение (сумма элементов постолбцу).
Полнота рассчитывается как количество объектов, корректно отнесенных к данному классу, к общему числу объектов данного класса (сумма по строке). Для приведенных выше примеров матрицы ошибок будут выглядеть вот так (см. таблицу 1).
Таблица 1. Матрицы ошибок для примеров
| Период 1 |
Выдача |
Отказ |
Не ясно |
Полнота |
|
| Выдача |
50 |
10 |
5 |
50/65 |
Средняя точность – 0,79 |
| Отказ |
10 |
30 |
5 |
30/45 |
Средняя полнота – 0,72 |
| Не ясно |
0 |
0 |
0 |
0/0 |
Точность в целом – 0,72 |
| Точность |
50/60 |
30/40 |
0/10 |
80/110 |
F-мера по среднему – 0,38 |
| Период 2 |
Выдача |
Отказ |
Не ясно |
Полнота |
|
| Выдача |
30 |
5 |
30 |
30/65 |
Средняя точность – 0,83 |
| Отказ |
5 |
20 |
20 |
20/45 |
Средняя полнота – 0,56 |
| Не ясно |
0 |
0 |
0 |
0/0 |
Точность в целом – 0,45 |
| Точность |
30/35 |
20/25 |
0/50 |
50/110 |
F-мера по среднему – 0,33 |
| Период 3 |
Выдача |
Отказ |
Не ясно |
Полнота |
|
| Выдача |
50 |
15 |
0 |
50/65 |
Средняя точность – 0,72 |
| Отказ |
15 |
30 |
0 |
30/45 |
Средняя полнота – 0,72 |
| Не ясно |
0 |
0 |
0 |
0/0 |
Точность в целом – 0,72 |
| Точность |
50/65 |
30/45 |
0/0 |
80/110 |
F-мера по среднему – 0,36 |
Мы можем также рассчитать точность алгоритма принятия решений в целом как сумму элементов на диагонали к сумме всех элементов матрицы. Полнота же для алгоритма в целом может быть рассчитана как среднее значение полноты для всех классов.
Построенная матрица называется матрицей ошибок. Она позволяет оценить не только точность системы в целом, но и те места, где система допускает больше всего ошибок. Например, видно, что для повышения точности во всех примерах нам необходимо уделять больше внимания ложной выдаче кредита.
Например, это может означать, что если у нас есть два алгоритма принятия решения и один из них точно выделяет «хороших» клиентов, а второй – «плохих», то мы можем взять ихкомбинацию. Если первый алгоритм говорит, что надо давать, – будем давать; если второй предлагает отказать – будем отказывать.
А вот если первый предложит отказать, а второй выдать (или с точностью до наоборот), то мы должны растеряться и предложить принять окончательное решение менеджеру более высокого звена. Или можно посмотреть на точность каждого из алгоритмов и поверить тому, у кого она больше.
Вместе с пониманием работы системы к нам приходит понимание, что точность истинных и ложных срабатываний связана между собой. Листая справочники, наш аналитик находит ROC-кривую.
Она показывает зависимость истинно положительных ответов с ложно положительными. Вновь рассмотрим две крайние ситуации. Если мы отказываем всем, то число как истинно положительных, так и ложно положительных решений равно нулю.
Если мы выдаем кредиты всем, то оба числа равны единице (мы выдали кредиты всем, кому надо, но и всем, кому не надо).
Если мы принимаем решение, бросая монетку, то оба числа будут изменяться пропорционально проценту принимаемых решений. Следовательно, для случайного принятия решений мы получим линию, похожую на прямую, соединяющую точки (0;0) и (1;1) (штриховая линия на рис. 1).
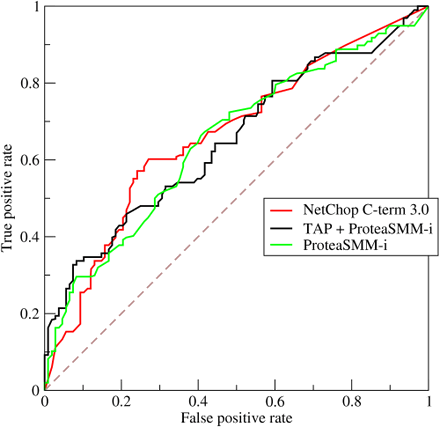
Рисунок 1. Пример ROC-кривых (изображение взято с сайта Википедия – https://ru.wikipedia.org/wiki/ROC-кривая)
Если мы хотим немного вредить, наша ROC-кривая окажется ниже, чем данная диагональ. Если мы построим идеальную систему, то от нуля она резко бросится вверх и дальше будет оставаться около 1.
Для численной оценки может использоваться показатель AUC (Area Under Curve). Для случайного процесса он будет равен 0,5; для идеальной системы – близок к 1; значение AUC для диверсанта будет стремиться к 0.
Таким образом, если мы хотим подстроить параметры нашей системы, надо оценивать значение AUC и выбирать тот алгоритм классификации, который дает наибольшее значение.
Здесь я не буду строить ROC-кривые для наших трех гипотетических случаев, так как они требуют варьирования параметров. В принципе ROC-кривую можно построить и дляотдельного сотрудника.
Например, мы можем имитировать отказ сотрудника (системы) от принятия решения, случайно выбирая заданный процент из ранее принятых решений. Этот процесс можно провести несколько раз, выбирая различные случаи (для этого и нужен случайный выбор). Далее можно подсчитать среднее для всех построенных кривых, усреднив по каждой източек по оси X. После этого можно сравнивать системы по вот таким усредненным данным.
Обратите внимание, что все численные показатели, рассчитанные с помощью матрицы ошибок, отличаются от тех же показателей, но рассчитанных в начале статьи. Также отличаются значения для средней точности и точности в целом.
Относительно этого можно сказать, что существует несколько методик расчета точности, которые дают различные значения. В связи с этим нельзя сравнивать между собой числа, полученные по разным методикам. Более того, как и в нашем случае, ранжирование методов может зависеть от методики оценки точности, то есть метод, являющийся лучшим сточки зрения одной методики оценки, может быть потеснен с пьедестала в другой методике.
Расчет показателей по матрице ошибок является методически более корректным. Анализ матрицы ошибок позволяет нам стандартизовать процесс нахождения «слабого звена» впринятии решений.
Представим себе, что расчет показателей качества работы нашего банка ведется исходя не из трех, а из четырех классов: все в порядке, небольшие проблемы с оплатой кредита, большие проблемы с оплатой кредита, отказ от принятия решения. В этом случае методика расчета матрицы ошибок останется той же. И точно так же мы сможем найти место валгоритме принятия решений, где совершается больше ошибок.
Кроме того, мы можем заставить менеджеров принимать решение по каждому из запросов на кредит. В таком случае становится не совсем очевидным, как считать полноту принятых решений без матрицы.
Матрица ошибок может использоваться в любой задаче классификации, кластеризации или вообще принятия решений. Аналогичным образом мы можем оценивать точность диагностики пациентов врачами, выявления брака в изделиях и любых других задачах, то есть метод универсален.
Предлагаемые числовые оценки позволяют оглянуться назад и понять, насколько хорошо или плохо мы принимали решения в прошлом. Пользуясь случаем, мне хотелось бы бросить взгляд на прошедший год, ведь вместе с ним заканчивается и эта серия статей.
В среднем раз в два месяца мы задумывались о том, как повысить обоснованность принятия решений, не прибегая к слишком сложным методам. Для начала (см. «БИТ», №3, 2016 – http://bit.samag.ru/archive/article/1658) мы рассмотрели некоторые методы из теории принятия решений, убедившись тем самым, что математика может пригодиться в случаях, когда не ясно, какой из имеющихся вариантов выбрать.
В следующей статье (http://bit.samag.ru/archive/article/1678) и следующем номере мы убедились, что красивая картинка в презентации имеет не только эстетическую ценность. Грамотно подобранная визуализация (и система координат) помогает увидеть как картину в целом, так и ее фрагменты. Заодно мы убедились, что показать шестимерное пространство на плоскости все-таки возможно.
В шестом номере «БИТа» (http://bit.samag.ru/archive/article/1719) мы научились оценивать расстояния между возможными решениями, даже если они не могут быть нанесены нагеографическую карту. Параллельные миры существуют не только в другой вселенной.
Если у нас есть несколько параметров, значит, у нас в руках новое многомерное пространство, в котором расстояния между объектами можно измерять по-разному (все зависит отрешаемой задачи). Кстати, для нового случая можно находить ближайший объект, для которого решение уже было принято, и считать, что в новом случае можно поступать точно также.
В двух предыдущих статьях (http://bit.samag.ru/archive/article/1734, http://bit.samag.ru/archive/article/1745) мы узнали, что если объекты нужно раскладывать по кучкам, то это задача классификации (и тоже задача принятия решений) или кластеризации.
Классификация хороша тем, что все объекты в классе считаются сходными, поэтому можно один раз решить, что с ними делать, и потом уже не мучиться с выбором. Если разделение на классы не известно, можно прибегнуть к кластеризации, которая сама разделит наши объекты на группы.
Наконец, в данной статье мы узнали, каким образом можно оценивать качество работы нашего метода принятия решений. Это позволяет вовремя скорректировать процедуру и(будем надеяться) улучшить свои показатели.
Все получилось стройно и логично, я даже не думал о таком, когда писал первую статью.
В заключение я хотел бы поблагодарить читателей, заинтересовавшихся методами принятия решения. Также хотелось бы поблагодарить журнал «БИТ» за возможность изложить накопившийся опыт в популярной форме.
Помимо этого, хотелось бы поблагодарить Российский научный гуманитарный фонд за стимулирование к практическому применению этих методов и финансирование в рамках гранта 15-04-12019.
Надеюсь, что в 2017 году приобретенные знания в области принятия решений помогут вам быть убедительными и успешными. Хочется пожелать читателям «БИТа» счастья иуспехов и вслед за героями «Кавказской пленницы» воскликнуть в новогоднюю ночь: «Так выпьем же за кибернетику!»
1 Мы уже разбирали классификацию в статье, опубликованной в «БИТ», №7, 2016 – http://bit.samag.ru/archive/article/1734.
2 В ходе редактирования коллеги подсказали мне, что брать произведение F-мер для разных классов является наиболее правильной стратегией. В начало⇑
Facebook
Мой мир
Вконтакте
Одноклассники
Google+
Комментарии отсутствуют
Комментарии могут отставлять только зарегистрированные пользователи
|
Вакансии на сайте Jooble
|
_cover.jpg)
