|
Календарь мероприятий
апрель  2024
Пн |
Вт |
Ср |
Чт |
Пт |
Сб |
Вс |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | | | | | |
показать все 
Новости партнеров
Сообщество цифровых управленцев «я-ИТ-ы» проводит ЗАКРЫТУЮ встречу в рамках выставки «Связь-2024»!
Читать далее
Ассоциация разработчиков «Отечественный софт» отметила 15-летие
Читать далее
РДТЕХ представил Технологическую карту российского ПО 2023
Читать далее
RAMAX Group получила партнерский статус уровня Gold по продукту Tarantool
Читать далее
показать все
Статьи
5 способов повысить безопасность электронной подписи
Читать далее
Как искусственный интеллект изменит экономику
Читать далее
Неочевидный САПР: выход ПО за рамки конструкторской деятельности
Читать далее
Скоро некому будет делать сайты и заниматься версткой
Читать далее
Цифровая трансформация в энергетике: как запустить проект с максимальным финансовым эффектом?
Читать далее
Мотивируй, не то проиграешь!
Читать далее
В 2024 году в России и мире вырастут объемы применения AR/VR
Читать далее
Цифровые технологии: надежды и риски
Читать далее
Будут ли востребованы услуги технической поддержки софта Oracle в России в ближайшие годы?
Читать далее
Здания с признаками интеллекта. Как Сергей Провалихин автоматизирует дома и производства
Читать далее
показать все
|
Выбери группировки объектов и выяви из них лучшую
Главная /
Архив номеров / 2016 / Выпуск №07 (60) / Выбери группировки объектов и выяви из них лучшую
Рубрика:
ИТ-управление
Facebook
Мой мир
Вконтакте
Одноклассники
Google+
Эдуард Клышинский, к.т.н., доцент департамента компьютерной инженерии НИУ ВШЭ
Выбери группировки объектов
и выяви из них лучшую
Есть несколько базовых принципов, владение которыми помогает повысить обоснованность принимаемых решений1
 В отличие от Шуры Балаганова старик Паниковский знал толк в деньгах. И, когда делил украденные у Корейко тысячи, он раскладывал купюры в соответствии с определенной закономерностью. При принятии решений правильная группировка объектов тоже является важным делом.
Распределив объекты по кучкам, мы сокращаем количество рассматриваемых сущностей и за счет этого упрощаем анализ. В данной статье рассмотрим несколько методов, помогающих выделять закономерности в группировке объектов и применять эти закономерности к новым объектам.
Расположение объектов по группам называется классификацией. Под объектами понимаются совершенно разные вещи: ситуации, события, объекты реального мира. Их объединяет то, что все они могут быть описаны с использованием некоторого фиксированного набора параметров. Как мы уже знаем, если объект описывается набором параметров, то мы можем измерить расстояние между данными объектами. Используя эти расстояния, можно делать выводы о том, насколько сходны имеющиеся объекты и относятся ли они к одному классу.
Классическим примером здесь являются заемщики, приходящие в банк. Если мы научимся делить заемщиков на «хорошую» и «плохую» группы еще до того, как им выдали кредит, успешность работы нашего банка существенно возрастет. Классическим примером, включенным во все учебники, также являются самолеты, которые летят со стороны противника к нашим важным объектам. Надеюсь, всем очевидно, зачем нужно классифицировать приближающийся самолет в один из двух классов (свой или чужой) и принять по нему правильное решение.
Если каждому классу заранее приписывается соответствующее ему решение, то задача принятия решения существенно упрощается после классификации. Классификация объекта автоматически показывает, что надо делать в текущей ситуации. «Плохому» клиенту надо отказывать, «хорошему» жать руку и отсчитывать деньги; чужой самолет надо опустить на землю, свой пропустить. Весь мир делится на фиксированное число оттенков, для каждого из которых написана инструкция.
Перед тем, как проводить классификацию, мы можем взять множество объектов, для которых уже достоверно известен их класс. Например, кредитные истории заемщиков, возвращавших или не возвращавших займы, изображения своих и чужих самолетов.
При наличии кредитной истории будет множество прецедентов, о которых известно, какое было принято решение и было ли оно правильное. В случае с самолетами кто-то должен вольно или невольно поработать над составлением списка своих или чужих самолетов и их характеристик. Подобный подход называется обучением с учителем: есть кто-то, кто знает правильный ответ, и его знания можно использовать при обучении. Составленное множество используется для тренировки системы в принятии решений о классификации новых объектов. Таким образом, сначала тренируется классификатор, который потом используется для решения задачи классификации. И имейте в виду, обучение с учителем – это не только классификация.
Несмотря на то что сначала идет этап обучения, а потом этап классификации, термин часто подразумевает оба этапа сразу – все равно без обучения не будет и классификации.
Как мы уже выяснили в предыдущих статьях, объекты можно представить как точки в некотором многомерном пространстве. Например, если мы занимаемся недвижимостью, то помещения будут характеризоваться адресом, стоимостью, площадью, типом удобств и другими параметрами. Если взять пространство, задаваемое этими параметрами как осями, и отложить на них значения для конкретного помещения, мы получим точку, описывающую это помещение. Между этими точками можно рассчитать расстояние, используя один из существующих методов. То есть мы можем говорить о близости квартир не только с точки зрения адреса, но и с точки зрения их сходства.
Теперь представим себе, что некий инвестор решил вложить крупную сумму в девелоперский проект в своем родном городке, в котором последнее новое здание строилось в 60-х годах прошлого века, а капитальный ремонт зданий проводился в 80-х. Как вы думаете, как распределятся точки-квартиры в многомерном пространстве по завершении этого проекта? Правильно, здесь – старые квартиры, подешевле, здесь – новые, подороже.
Заметьте, для классификации нам может хватить единственного параметра – цены за квадратный метр. Это очень удобная ситуация. Кластеры расположены довольно компактно, а расстояние между кластерами велико. На практике такая ситуация скорее всего не встретится и нам придется работать с большим числом параметров, но ситуация может сохраниться. Несмотря на большое количество параметров, кластеры будут продолжать располагаться компактно, а расстояние между ними будет велико.
В такой ситуации для классификации можно применить следующий метод. Давайте считать, что у каждого кластера есть некоторый центр, определяемый как среднее арифметическое всех относящихся к нему точек. Тогда точка относится к тому кластеру, к центру которого она ближе (см. рис. 1). В самом деле, если цена за квартиру в нашем гипотетическом городке ближе к цене на новостройку, то и сама квартира скорее всего является новостройкой.
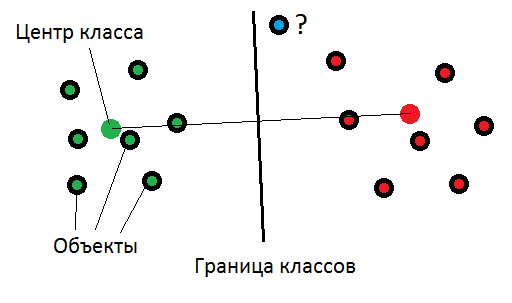
Рисунок 1. Граница между «красными» и «зелеными» проходит между центрами групп. «Синий» ближе к центру «красных» и будет отнесен к ним
Обучение здесь производится очень просто – нужно взять все точки одного кластера и найти их центр. Подобную операцию надо провести для каждого имеющегося у нас кластера.
В данном методе граница между кластерами будет проходить по прямой, проходящей через середину отрезка, соединяющего центры кластеров, и перпендикулярной этому отрезку. Если кластеров несколько, эти прямые будут пересекаться и превращаться в лучи или отрезки. При большом количестве кластеров мы получим картину, называемую диаграммой Вороного (см. рис. 2).
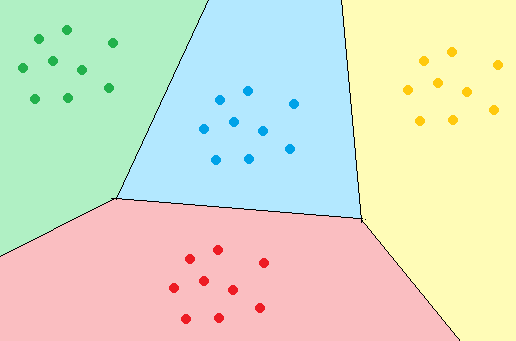
Рисунок 2. На диаграмме Вороного класс новой точки можно определить по цвету заливки
Каждая ячейка будет показывать все возможные точки своего кластера. Классификация в такой ситуации сводится к тому, чтобы понять, в какую клетку попадает новая точка. Для этого надо всего лишь понять, с какой стороны разделительной линии находится объект. Работа классификатора будет заключаться в том, чтобы понять, где находится новая точка относительно этой линии – выше или ниже (правее или левее).
Однако «поровну» не всегда означает «по справедливости» или «правильно». Представим себе, что один из кластеров значительно больше другого. В такой ситуации граница кластеров должна сдвинуться в сторону меньшего кластера исходя из следующей логики. Если граница будет проходить близко к точкам одного из кластеров, то предъявляемые нам для классификации объекты могут пересечь эту границу и классификатор даст ошибочный прогноз. Поэтому ширина «серой зоны», в которую не попала ни одна из точек обучающей последовательности, должна быть максимальна, а граница будет проходить по ее середине (см. рис. 3).
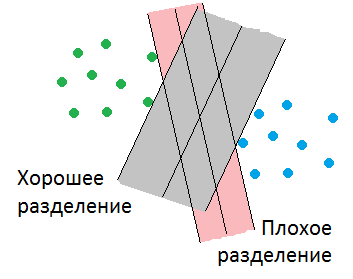
Рисунок 3. Серая полоса шире розовой, поэтому она надежнее разделяет два класса точек
Данный метод называется методом опорных векторов (Support Vector Machine, SVM). Теперь точка, отошедшая от своих товарок на небольшое расстояние, не окажется вдруг на территории чужого кластера. А если она отстоит достаточно далеко от точек кластера, то может быть она и в самом деле относится к другому классу?
Делить кластеры между собой можно не только прямыми. Представьте себе, что у вас есть забор с красными и зелеными штакетинами. Вы сможете разделить их с помощью прямой? А вот синусоида вполне подойдет. Но подбирать правильную синусоиду значительно сложнее, чем набор прямых. Опять-таки вдруг это не синусоида, а гиперболический тангенс в комбинации с поверхностью восьмого порядка и экспонентой?
Такие вещи можно подбирать, но только если в вашем распоряжении есть серьезный вычислительный кластер, много времени, большой опыт и огромное желание разобраться поточнее. В остальных ситуациях лучше потерять в точности, но быстро прикинуть с помощью прямых. Может оказаться, что SVM дает на вашей задаче не такой уж и хороший результат.
Можно применить и другой метод, попроще (но тоже не факт, что он нам подойдет). Если объект идет как кошка, выглядит как кошка и мяукает как кошка, то может быть это и есть кошка? Точнее, так: если объект похож на Барсика, Персея и Пушка, но не похож на Шарика, Тузика и Дымку, то скорее всего это кот.
Или в более общем случае, если объект имеет по соседству больше точек одного кластера, чем точек других, то его следует отнести к этому первому кластеру (см. рис. 4). Для этого не обязательно проверять все точки всех кластеров, достаточно взять лишь k самых близких к проверяемому объекту. По этому магическому k метод так и называется – «k ближайших соседей».
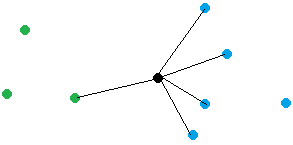
Рисунок 4. Четыре из пяти ближайших точек – «синие». Новая точка будет отнесена к этому классу
Плюсом метода является разделение классов не прямыми, а сложными линиями, форма которых зависит от взаимного расположения точек и выбора k. Желательно, чтобы k не было кратно числу имеющихся кластеров, так как в противном случае возможна ситуация, когда точки распределятся равномерно. Вообще в качестве k лучше взять простое число, большее числа кластеров, так как всегда возможна ситуация, в которой из семи кластеров в соседях у нас окажутся только два или три.
В литературе описывается ситуация, когда от выбора k зависит результат классификации. Увеличивая k, мы присоединяем точки других классов и тем самым меняем результат. На это можно сказать одно. Если кот поймал собаку, значит, это была крыса, что бы там ни кричала хозяйка собаки. Ошибки классификации возможны всегда, поэтому надо принять некоторое решение относительно k и дальше стойко его придерживаться. В конце концов k можно подобрать в результате нескольких экспериментов.
Но давайте вернемся к нашему гипотетическому городку. В самом начале мы описали ситуацию, в которой анализ стоимости квадратного метра позволял нам безошибочно определить, где находится помещение – в новой части города или в старой. На практике подобная ситуация вряд ли будет иметь место. Скорее всего у новостроек будет какая-то совсем уж окраина подешевле, а в старой части города будет престижный центр, близкий ко всем благам цивилизации и сопоставимый по цене с новостройками (а скорее всего и дороже, чем окраина новостроек). То есть объекты будут достаточно плавно перетекать из одного класса в другой так, что нельзя будет провести такую прямую (а если параметров больше трех – гиперплоскость), когда все объекты новостроек окажутся с одной стороны, а все объекты старого города – с другой.
Давайте попробуем посмотреть на все параметры. Адрес? Если не с точностью до дома (это было бы слишком просто), то выяснится, что несколько новых домов были построены и в центре. Этажность? Похоже на правду. Старые дома были и мало- и многоэтажными, а новые только многоэтажные. Значит, если здание малоэтажное, то оно точно старое, а если многоэтажное, то вопрос остается открытым. Хм…
Но мы же можем посмотреть по цене: если квадратный метр стоит дорого, то это скорее всего новый дом. А если следом посмотреть размер квартиры в зависимости от количества комнат, то ситуация станет еще прозрачнее. И форма собственности дает определенные подсказки – до недавнего времени апартаменты не сдавались. Получается, что ни один из параметров сам по себе не может отличить старую квартиру от новой, но вместе они могут помочь найти правильный ответ. В такой ситуации могут помочь деревья принятия решений.
С деревьями принятия решений знакомы все, кто проходил тесты в виде дерева или графа, когда в вершине написан вопрос, а дальше идет несколько стрелок к другим вершинам (см. рис. 5). В них есть вершины с вопросами, есть стрелочки со значениями, которые ведут из вершины в вершину, и есть вершины, показывающие класс объекта. Прекрасная визуализация методов анализа данных и алгоритма работы деревьев принятия решений дана на сайте http://www.r2d3.us.
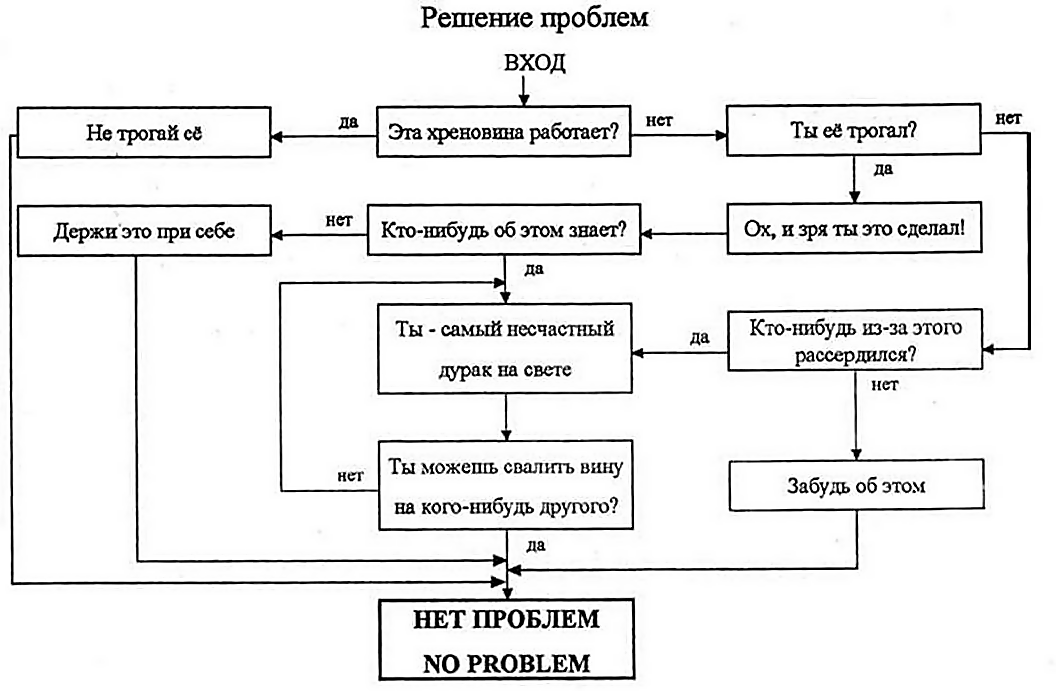
Рисунок 5. Дерево принятия решений для решения проблем (найдено на просторах интернета)
В нашем случае можно построить такое же дерево, которое будет относить квартиры к одному из двух классов: квартира находится в новостройке или в старой застройке. Это апартаменты: Да/Нет? Да. Тогда это новостройка. Нет. Какова стоимость квадратного метра? Вариант 1 – это старый город, больно дешево. Вариант 2 – это новостройка, больно дорого. Вариант 3 – думаем дальше. И так далее до тех пор, пока мы не придем к решению.
Для построения таких деревьев существует несколько алгоритмов, например ID3 или C4.5. Давайте кратко рассмотрим их суть.
У нас имеется набор объектов, для каждого объекта заданы значения всех параметров. С какого параметра начать рассмотрение классификации? Конечно же, с того, который лучшим образом разделяет наше множество на классы! Но сначала давайте разберемся, что такое хорошо, а что такое плохо.
Отлично – это когда каждый ответ выделяет объекты только одного класса. У нас в руках несколько объектов двух классов. Нас спрашивают, есть ли какой-то признак у этих объектов. Если мы отвечаем «да», то у нас остаются только объекты первого класса, если отвечаем «нет», только второго (мальчики направо, девочки налево; объекты разделились, решение найдено). Хорошо – когда ответ выделит много объектов одного класса и примешает к ним чуть-чуть объектов других классов (мы надеемся разделить их следующим вопросом). Плохо – когда объекты распределены по классам равномерно (в такой ситуации мы слабо приближаемся к пониманию ответа). Значит, в качестве метрики можно взять, например, разницу между количеством объектов из разных классов, прошедших по одной ветви. Чем эта разница больше, тем разделение лучше.
Итак, у нас есть множество объектов, на которых проводится обучение. Для каждого параметра (вопроса) оцениваем качество разделения этого множества на подмножества. Выбираем параметр с наилучшим показателем. Данный параметр разбивает наше множество на несколько подмножеств, привязанных к ответам (значениям параметров).
Повторим операцию для каждого из подмножеств. Возьмем все параметры (кроме того, что уже брали), посмотрим, где разделение подмножества будет наилучшим, разделим объекты по нему. Снова возьмем одно из множеств и снова попробуем его разделить. Деление будет производиться до тех пор, пока в множестве не останутся объекты только одного класса. В этой вершине можно писать ответ – раз вы пришли сюда, то ваш объект относится к вот этому классу.
А что делать, если параметры кончились, а объекты все еще принадлежат разным классам? Это плохая ситуация: или задача не решается строго, или мы выбрали не те параметры (сложно решать, надо покупать или продавать в зависимости от светимости Альголя, надо было выбрать другой показатель).
Такую ситуацию мы рассматривать сейчас не будем. Как и не будем рассматривать истинную суть методов ID3 и C4.5. Я ведь еще не рассказывал об информационной энтропии? Ну, тогда давайте отложим более подробное объяснение до лучших времен. Пока достаточно знать, что такие методы есть и работают лучше, чем то, что я вам сейчас рассказал.
Еще одним мощным методом является регрессия. Давайте для простоты предположим, что все наши параметры являются числовыми (или сводятся к ним). Теперь давайте построим линейную функцию, в которую эти параметры будут входить с некоторыми коэффициентами (умножим каждое значение параметра на некоторый коэффициент и сложим все произведения). Теперь подберем коэффициенты таким образом, чтобы все объекты одного класса давали значения больше некоторого порога, а все объекты второго класса – меньше этого порога.
Если нам повезло и у нас получилось, то – тадам! – у нас есть классификатор на основе линейной регрессии. Обучение такого классификатора сводится к подбору коэффициентов, классификация – к расчету одного числа по некоторой функции и сравнению его с другим.
На самом деле эта функция не обязана быть линейной. Если в состав функции параметры входят в какой-то степени, то все равно говорят о линейной регрессии. На практике часто используют логистическую регрессию, основанную на возведении в степень экспоненты. Но суть метода от этого не меняется: значение выше порога – один класс, ниже порога – другой.
Логистическая функция удобна тем, что дает значения от 0 до 1. Это дает возможность сравнивать между собой значения, полученные для разных функций. Зачем?
Регрессия делит объекты только на два класса. Если классов больше, можно, например, построить для каждого класса свой классификатор. Когда мы предъявим новый объект, какое-то количество классификаторов откажется опознавать его как принадлежащий соответствующим классам. Если объект «признает» только один классификатор, решение найдено.
Если «отзовутся» несколько, то мож-но отдать объект тому классу, чей классификатор выдаст максимальное значение. Вместо стратегии «победитель получает все» можно строить классификатор результатов, выдаваемых классификаторами более низкого уровня, или выбрать какой-нибудь другой метод.
Методов гораздо больше, чем мы уже рассмотрели в этой статье. Я ничего не сказал о нечеткой классификации (которая на самом деле сводится к тому, что мы выдаем не номер класса, а степень уверенности для каждого из классов, что объект принадлежит именно ему).
Мы не рассмотрели случайный лес, который скрещивает пальцы и строит неплохой классификатор по плохим данным. Мы не рассмотрели такие подходы, как бэггинг и бустинг, которые позволяют улучшить точность классификации. В статье до этой строчки ни разу не упоминались нейронные сети.
Мы даже не обсуждали, что такое эта самая точность и как ее мерить. Мы не говорили о том, что делать с плохими данными. Может быть, в другой раз. Но рассмотренный материал может помочь правильно принять решение о том, какой метод классификации использовать и использовать ли вообще. Можно даже попробовать их все, благо теперь это можно сделать достаточно быстро при наличии правильных программных средств. И эти средства служат для того, чтобы мы с вами принимали решения более обоснованно и быстро. Хотя анализ данных и требует времени. Хотя бы на выбор и составление модели.
1 Автор все еще признателен Катерине Ляско за идею названия и аннотации данной статьи (см. «БИТ», №1, 2 и 3/2016). В начало⇑
Facebook
Мой мир
Вконтакте
Одноклассники
Google+
Комментарии отсутствуют
Комментарии могут отставлять только зарегистрированные пользователи
|
Вакансии на сайте Jooble
|
_cover.jpg)
