|
Календарь мероприятий
ноябрь  2024
Пн |
Вт |
Ср |
Чт |
Пт |
Сб |
Вс |
| | | | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
показать все 
Новости партнеров
Обновление BI.ZONE Secure DNS: гибкая настройка фильтрации и максимальная скорость
Читать далее
RED Security: в октябре количество DDoS-атак на ТЭК выросло в 3 раза
Читать далее
Falcongaze представила новую версию DLP-системы — SecureTower 7 Helium
Читать далее
ИСП РАН покажет результаты 30-ти лет работы на Открытой конференции в Москве
Читать далее
Юбилейная конференция ЭОС: ЭОС: 30 лет лидерства на рынке автоматизации документооборота и обсуждение актуальных трендов
Читать далее
показать все
Статьи
Тандем технологий – драйвер инноваций.
Читать далее
ИИ: маршрут не построен, но уже проектируется
Читать далее
Глеб Шкрябин: «Надежные и масштабируемые системы — основа стабильной работы бизнеса в условиях больших нагрузок»
Читать далее
Елена Ситдикова: «На разработчиках программного обеспечения для транспорта лежит большая ответственность перед пассажирами»
Читать далее
Технологический ИИ-арсенал
Читать далее
Взгляд в перспективу: что будет двигать отрасль информационной безопасности
Читать далее
5 способов повысить безопасность электронной подписи
Читать далее
Как искусственный интеллект изменит экономику
Читать далее
Неочевидный САПР: выход ПО за рамки конструкторской деятельности
Читать далее
Скоро некому будет делать сайты и заниматься версткой
Читать далее
показать все
|
Пусть компьютер сам выберет группировки объектов и выявит из них лучшую
Главная /
Архив номеров / 2016 / Выпуск №08 (61) / Пусть компьютер сам выберет группировки объектов и выявит из них лучшую
Рубрика:
ИТ-управление
Facebook
Мой мир
Вконтакте
Одноклассники
Google+
Эдуард Клышинский, к.т.н., доцент департамента компьютерной инженерии НИУ ВШЭ
Пусть компьютер сам выберет
группировки объектов и выявит из них лучшую
Есть несколько базовых принципов, владение которыми помогает повысить обоснованность принимаемых решений1
 В тот момент, когда Сьюзен Келвин, Главный Робопсихолог и Главный Математик фирмы «Ю.С. Роботс энд Мекэникл Мен Корпорейшн», искала затерявшегося среди других робота по имени Нестор Десять, она решала задачу классификации: есть обычные роботы, и есть Нестор Десять, который отличается от них по характеристикам. Однако хитроумный робот тщательно скрывал свои способности и делал все для того, чтобы классификация давала погрешность. Классификатор было невозможно обучить, так как для негоне было обучающей выборки.
Как и у Сьюзен Келвин, у нас в руках может оказаться набор данных, в котором объекты не будут заранее распределены по классам. Между тем нам нужно будет понять, как можно разделить имеющиеся объекты на несколько групп, в которые попадут сходные объекты. В такой ситуации говорят не о классификации, а о кластеризации. Задачей кластеризации является разделение объектов на некоторое (возможно, заданное заранее) число классов, пользуясь лишь значениями их параметров.
Возможно ли такое разделение? Возможно, но сначала давайте разберемся, зачем оно может быть необходимо.
В прошлый раз я приводил пример с клиентами банка. У банка есть обширная информация о своих заемщиках и приписанный к ним «класс проблемности»: кредит был возвращенбез проблем, имели место мелкие или проблемные просрочки, кредит не был выплачен. Теперь представим себе, что банк не имеет информации о том, как выплачивается кредит.Как такое возможно?
Приведем другой пример. Мы сделали партию новых изделий. Еще до начала эксплуатации нам нужно понять, как они будут работать. Просто посмотреть, насколько они близки кзаданным в документации параметрам, нельзя, мы можем отсеять изделия, которые сделаны ближе к реальным условиям эксплуатации и будут работать лучше. В этом случае можно попытаться выделить группы похожих друг на друга изделий и рассматривать их уже в рамках групп – например, провести тестовую эксплуатацию одного изделия из группы ипредположить, что остальные члены группы будут вести себя точно так же. Это будет стоить значительно дешевле, а мы получим возможность свести определение качества изделийк классификации, так как у нас появится возможность работать с полученными классами.
Помимо этого, мы можем решать другую задачу. Известно, что среди наших деталей постоянно встречаются бракованные. Каковы причины возникновения брака? Теоретически возможно несколько вариантов: некорректная настройка части оборудования, невысокая квалификация рабочих, некорректная работа отдела приемки. Возможна и комбинация некоторых признаков.
Если мы сумеем сгруппировать объекты таким образом, что в одной из групп процент брака будет значительно выше, чем в других, это будет означать, что мы нашли самый существенный источник брака. Проанализировав параметры, задающие группу с высоким уровнем брака, мы сможем принять правильное решение об управляющем воздействии, которое должно будет улучшить ситуацию.
Итак, кластеризация может использоваться для решения двух задач: разделение объектов на группы для последующего решения задачи классификации (1) и исследование структуры системы за счет группировки объектов (2).
В первом случае у нас имеется множество объектов, известны их характеристики, и нам необходимо разделить их на группы. Как и в случае классификации, в качестве объектов могут быть совершенно разные сущности: пользователи, для которых мы хотим выявить предпочтения; слова, которые мы хотим сгруппировать по общему признаку; поведение пользователей и так далее. Мы не знаем самих групп, мы не знаем, к какому классу принадлежат объекты, но мы хотим разделить их по сходству признаков на группы и дальше обрабатывать уже по группам.
Моим любимым примером для второго случая является студенческая работа, в которой исследовалась эффективность применения двух лекарств от рака в зависимости от различных параметров пациентов.
В ходе кластеризации врачебных данных было выделено несколько групп пациентов со сходными признаками, для которых в основном применялось одно из лекарств и наблюдалось снижение числа летальных исходов. Наблюдения позволили уточнить выбор лекарства в определенных случаях и сократить общую смертность. Да, число пациентов в этих кластерах составило всего лишь 10-20% от общего количества, но корректный выбор лекарства для этой группы увеличивал шансы на выживание в несколько раз. Неплохой результат для студента-программиста. И хороший пример исследования структуры системы за счет выделения кластеров сходных объектов.
Для того чтобы понять, что объекты сходны, надо научиться определять расстояние между ними. Для этого надо зафиксировать множество признаков и выбрать одну из метрик, рассмотренных в одной из прошлых статей. Итак, все объекты расположены в некотором многомерном пространстве, и мы можем рассчитать расстояния между ними.
Самым простым решением в таком случае будет взглянуть на взаимное расположение объектов, использовав визуализации данных (этот вопрос мы уже тоже рассматривали). Выбрав один из методов отображения, мы выводим получившуюся картинку на экран и видим, что в правом нижнем углу у нас собралась одна группа точек, а в левом верхнем – другая, амежду группами можно провести прямую, разделяющую эти два класса.
Идеальная ситуация, но на практике число параметров может оказаться слишком большим. В итоге у нас не получится сделать нормальную визуализацию и разделить объекты наглаз. Но давайте пока не будем отказываться от этой идеи. Кластеры и в самом деле могут оказаться компактными и легко отделимыми, даже в пространстве большой размерности, пусть мы и не увидим этого на глаз.
В прошлый раз мы разбирали метод классификации, в котором рассчитывался центр класса как среднее арифметическое всех его точек. Дальше для того, чтобы понять, какому классу принадлежит объект, нам было нужно просто найти самый близкий центр класса из всех, и отнести объект к этому классу. Может быть, мы можем найти эти центры исходя изкаких-то простых соображений?
Пусть мы знаем, что число кластеров равно k. Тогда, если у нас получится расположить k точек в пространстве признаков таким образом, чтобы они являлись центрами соответствующих кластеров, задача будет решена. Для этого сначала расположим эти k точек случайным образом, а дальше будем сдвигать их так, чтобы они все лучше и лучше описывали центры соответствующих кластеров.
Давайте мы даже немного схитрим на первом этапе (это будет называться «расположить точки псевдослучайным образом») и в качестве начального приближения возьмем точки, максимально удаленные друг от друга. Тогда на следующих шагах эти точки будут смещаться поближе к середине, пока не станут настоящими центрами кластеров.
Для того чтобы понять, куда смещать центральные точки, для каждого из объектов найдем самую близкую к нему точку центра. За счет этого все объекты разделятся на k групп. Теперь рассчитаем истинный геометрический центр для каждой из групп, переместим центральную точку в него, а после этого снова разобьем объекты на k групп по их близости кцентральным точкам.
Если нам повезло и изменение границ групп не повлияло на принадлежность объектов к группам, кластеризация закончена. Центральная точка больше не будет менять своего положения, и мы надеемся, что она будет хорошим приближением для истинного центра кластера. Кластеризация окончена, теперь можно использовать полученные точки центров кластеров для классификации новых объектов или изучения свойств самих полученных групп.
Если же в ходе смещения центров нам не повезло и распределение объектов изменилось, то мы повторяем операцию сначала: пересчитываем принадлежность объектов группам, рассчитываем новый центр, проверяем изменение группировки. В подавляющем большинстве случаев процесс сходится (см. рис. 1).
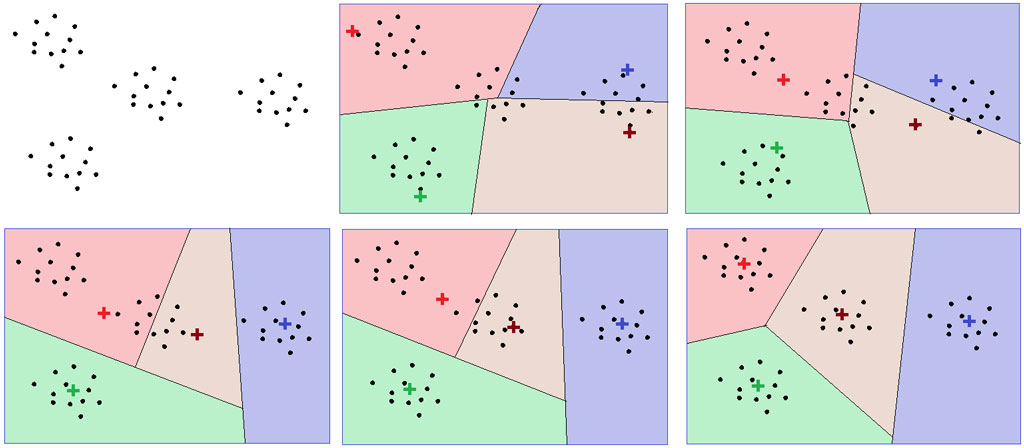
Рисунок 1. Разделение точек на кластеры методом k-средних
Замечу, что процесс сойдется, даже если мы выберем начальные точки случайным образом, главное, чтобы они не совпадали. Если точки будут находиться близко друг к другу, онибыстро разойдутся на первом шаге, после чего ситуация будет сходной. А выбирать в качестве начальных точек имеющиеся объекты проще, чем генерировать их заново. По крайней мере генерировать их в разнородном миллиономерном пространстве.
Более того, выбирать наиболее удаленные друг от друга точки может оказаться значительно дороже, чем проводить саму кластеризацию. Поэтому обычно случайным образом выбирают k объектов из множества данных и начинают кластеризацию от них.
Данный метод называется методом k-средних (не путайте с методом кластеризации k ближайших соседей). Он очень прост в реализации и быстро работает, отчего и пользуется большой популярностью. Но у него есть и недостатки.
Во-первых, для метода k-средних необходимо подбирать значение k, хотя для этого есть несколько простых, но вычислительно затратных методов.
Во-вторых, он хорошо работает лишь для компактных и далеко разнесенных кластеров, а для скученных и пересекающихся кластеров работает хуже (но все еще работает).
И, в-третьих, метод не может выделить кластеры сложной формы – только выпуклые многоугольники или многогранники.
Для подбора k необходимо провести несколько экспериментов с различными значениями k и выбрать из них лучший результат. Результат оценивается по-разному. Можно визуализировать данные и посмотреть на результат (когда объекты раскрашены в цвета своих классов, их легче анализировать). Можно использовать специальную формулу, которая требует, чтобы размеры кластеров были как можно меньше, а расстояния между ними как можно больше. Наконец можно оценить устойчивость разбиения.
Представим себе, что у нас есть данные, относящиеся к трем хорошо отделимым кластерам. Если мы выберем k=3, то, как ни разбивай, два объекта, относящиеся к одному и тому же классу, всегда будут оказываться в одном и том же кластере. Чтобы убедиться в этом, достаточно провести несколько экспериментов.
Если же мы выберем k=4, то либо один из трех кластеров будет делиться пополам, либо «лишний» кластер будет отбирать на себя объекты сразу из двух классов. А так как мыначинаем со случайной точки (вот зачем еще нужен именно случайный выбор), то «лишний» кластер будет «гулять» по нашим данным, что будет видно в результатах кластеризации.При k=2 два класса из трех будут объединяться, но тоже случайным образом.
Таким образом, неправильный выбор k приводит к тому, что результаты нескольких прогонов метода на одних и тех же данных будут различаться. Правда, при k=6 ситуация вновь стабилизируется, как и при k=9. То есть, если вы получили стабильное разбиение при числе кластеров, не равных простому числу, попробуйте провести кластеризацию на его делителях.
Если классы не находятся друг от друга на большом расстоянии, а пересекаются, стабильная картина может не наблюдаться никогда. В зависимости от того, какие начальные точкимы выбрали, итоговые кластеры будут выглядеть немного иначе.
Однако часть точек всегда будет попадать в один и тот же кластер. То есть посреди общего хаоса будут наблюдаться острова стабильности. В этом случае k следует выбирать исходяиз того, насколько стабильным остается разбиение. Да, не для всех точек мы можем точно сказать их класс, но мы постараемся увеличить их число.
Итак, метод k-средних позволяет довольно просто провести кластеризацию объектов. При помощи некоторых вычислительных затрат мы можем подобрать правдоподобное значение k. Однако метод стабильно работает только для хорошо разделимых кластеров.
Для «неудобных» данных улучшить ситуацию можно, перейдя к методам, основанным на плотности. Взглянем на рис. 2. Сколько на нем кластеров? Ответ может варьироваться – отодного до десятка (а мы продаем или покупаем?).
Рисунок 2. Пример данных с трудно разделимыми кластерами
Логика рассуждений может быть следующая. Найдем место с самой большой плотностью точек. Несколько самых близкорасположенных точек станут «основой» для создания нового кластера. Теперь давайте присоединим к ним те точки, что недалеко лежат от этой «основы». Дальше присоединим те, что лежат близко от получившегося множества.
Будем присоединять точки до тех пор, пока точки, лежащие близко от растущего кластера, не закончатся. Получившееся множество объектов назовем кластером и попытаемся выделить следующий: найдем близко расположенные точки, добавим к ним те, что лежат рядом, и т. д.
Подобным образом работает, например, метод DBSCAN. Он обладает массой плюсов: нет необходимости подбирать число кластеров (метод находит их сам), кластеры могут быть сложной формы, кластеры могут частично перекрываться. Минусов тоже немало, например метод вычислительно сложнее. Но это не так страшно. Ну, по крайней мере до тех, пока вы не пытаетесь кластеризовать все население Китая.
Как было сказано выше, кластеризация используется для того, чтобы понять структуру имеющихся у вас данных.
В методе DBSCAN необходимо задать параметры: как близко должны располагаться точки «основы» кластера и каково максимальное расстояние до точки, присоединяемой ккластеру. Неверный выбор этих параметров либо приведет к тому, что все точки склеятся в один кластер, либо к тому, что кластеров станет слишком много, а сами они будут слишком маленькими. То есть, чтобы назначить эти параметры, надо знать структуру данных. Но мы-то используем кластеризацию, чтобы ее понять! Получается противоречие, которое можно разрешить путем экспериментального подбора параметров.
Но есть методы и получше. Например, параметры метода можно выбирать динамически. Например, в качестве «основы» кластера можно выбирать три точки с самым маленьким расстоянием. Решение о том, можем ли мы присоединить точку, можно принимать исходя из среднего расстояния между ближайшими соседними точками (если оно меньше среднего, то точку можно присоединить). Не всегда такой выбор будет наилучшим, но здесь можно добавить какие-то параметры, которые будут приводить модель к виду, который нравится нам больше.
Процедуру кластеризации можно упростить. Например, можно взять две самые близкие точки и объединить их, сказав, что теперь они составляют один кластер и будут рассматриваться вместе. Дальше мы находим следующие две точки (или точку и кластер, или два кластера), которые находятся на минимальном расстоянии, и объединяем их. Объединение ведется до тех пор, пока алгоритм не остановится. Только остановится он тогда, когда объединит все точки в один кластер, так как всегда есть два объекта, расстояние между которыми минимально.
Подобный метод позволяет построить дендрограмму – график, который показывает, на каком расстоянии находились объединяемые объекты.
По оси X находятся наши объекты данных, а по оси Y – расстояния (оси могут меняться местами). От каждого объекта параллельно оси Y идут линии. Как только линия доходит дотого расстояния, на котором объекты были объединены, мы рисуем горизонтальную линию, соединяющую «линии жизни» объектов, и от нее начинаем рисовать новую – линию получившегося кластера.
За счет этого всегда можно визуально оценить, когда объединялись объекты или кластеры и сколько кластеров при этом получалось. Так, по рис. 3 можно увидеть, что сначала объединились точки 3 и 6, потом 2 и 5, затем эти два кластера соединились вместе, захватив точку 4, а точка 1 присоединилась в последнюю очередь.
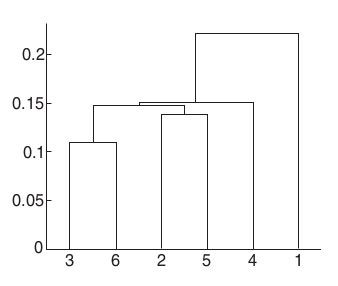
Рисунок 3. Пример иерархической кластеризации
Если мы захотим провести границы между кластерами, то логичным будет соединять или все точки, кроме 1, или только 3 и 6, так как расстояния между остальными кластерами отличаются незначительно.
Данный метод называется методом иерархической кластеризации. Он имеет два заметных недостатка и три модификации. Недостатки состоят в том, что метод является очень медленным (надо многократно рассмотреть расстояния между всеми точками) и не автоматическим (где проходят границы между кластерами, придется решать вручную, что прибольшом объеме данных очень неудобно).
Три модификации состоят в том, как рассчитывать расстояние до кластера: можно брать расстояния между ближайшими точками, между самыми дальними точками и между средними точками. Каждая из модификаций дает свои собственные результаты и отличающиеся дендрограммы.
Вообще получение разных результатов является в данной области нормальным явлением. На странице библиотеки кластеризации, входящей в состав пакета sklearn для языка Python, приведены изображения кластеров, получаемых различными методами (см. рис. 4).
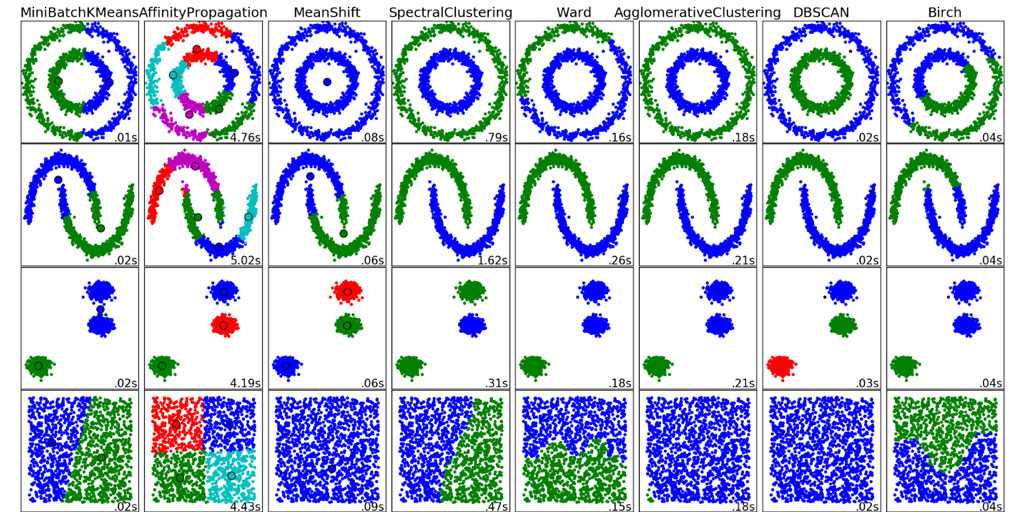
Рисунок 4. Результаты кластеризации различными методами из пакета sklearn (изображение взято с сайта пакета)
Как вы можете заметить, результаты разнятся значительным образом. Но так как этот пакет существует и он находится в свободном доступе, вы всегда можете попробовать несколько разных методов и выбрать из них тот, что дает результаты лучше.
По традиции в завершении я упомяну по названиям те методы, что мы не рассмотрели. Я несколько раз предлагал выбрать метод получше, но так и не рассказал, как его мерить. Может быть, опять в другой раз? Мы даже не коснулись методов нечеткой кластеризации, когда каждому объекту приписывается вектор значений, которые можно интерпретироватькак степень нашей уверенности, что этот объект принадлежит тому или иному классу. Здесь хотелось бы отметить метод FLAME, которому я лично симпатизирую, хотя некоторые предпочитают нечеткий вариант k-средних, называемый c-средних. Мы все время объединяли точки в один кластер. Однако существует совершенно другой подход, когда с самого начала все точки кладутся в один кластер, а потом мы пытаемся разделить его. Мы не сказали ни слова о методе Affinity Propagation и спектральной кластеризации.
Но я надеюсь, что вы поняли главное. Если у вас есть много данных, для которых нужно выделить классы, а никакой информации по принадлежности к классам нет, то надо использовать кластеризацию. Это поможет нам разобраться в структуре данных и принять правильное решение. Как? Например, с помощью классификации. А если не поможет иона, то с помощью интуиции. Но красивые картинки на основе визуализации результатов кластеризации мы всегда сможем предоставить.
1 Автор на протяжении уже долгого времени признателен Катерине Ляско за идею названия и аннотации данной статьи (см. «БИТ», №1, 3, 4, 6 и 7/2016).
2 Азимов А. Как потерялся робот. В начало⇑
Facebook
Мой мир
Вконтакте
Одноклассники
Google+
Комментарии отсутствуют
Комментарии могут отставлять только зарегистрированные пользователи
|
Вакансии на сайте Jooble
|
_cover.jpg)
_cover.jpg)
_cover.jpg)
_cover.jpg)
