|
Календарь мероприятий
декабрь  2025 2025
Пн |
Вт |
Ср |
Чт |
Пт |
Сб |
Вс |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | | | | |
показать все 
Новости партнеров
Более 40% российских компаний, переехавших в облако, используют мультиклауд
Читать далее 
STEP LOGIC внедряет ИИ для безопасной работы с корпоративными данными
Читать далее 
Чайная церемония: разговор о ЦОДах
Читать далее 
Цифровая платформа «СмартСпорт 2:0» включена в Реестр Минцифры
Читать далее 
«Группа Астра» раскрыла неаудированные финансовые и операционные показатели за 9 месяцев 2025 года
Читать далее 
показать все 
Статьи
Генеративный ИИ. Универсальный ИИ. Где место человека?
Читать далее 
Как продолжать расти в сложные времена?
Читать далее 
Поддержка 1С - "черная дыра" IT- бюджета: как превратить хаос в управляемый процесс и оптимизировать затраты
Читать далее 
Как посчитать реальную выгоду от ИИ в видеонаблюдении?
Читать далее 
Управление расходами: режем косты с помощью ИИ
Читать далее 
Точность до метра и сантиметра: как применяют технологии позиционирования
Читать далее 
Как искусственный интеллект изменит экономику
Читать далее 
Эпоха российской ориентации на Запад в сфере программного обеспечения завершилась
Читать далее 
Сладкая жизнь
Читать далее 
12 бизнес-концепций, которыми должны овладеть ИТ-руководители
Читать далее 
показать все 
|
Выбери расстояния между объектами и выяви из них оптимальное
Главная /
Архив номеров / 2016 / Выпуск №06 (59) / Выбери расстояния между объектами и выяви из них оптимальное
Рубрика:
ИТ-управление
Facebook
Мой мир
Вконтакте
Одноклассники
Google+
Эдуард Клышинский, к.т.н., доцент департамента компьютерной инженерии НИУ ВШЭ
Выбери расстояния между объектами
и выяви из них оптимальное
Есть несколько базовых принципов, владение которыми помогает повысить обоснованность принимаемых решений1
Подобно героям фильма «Человек с бульвара Капуцинов» можно смело утверждать: «Далека дорога твоя». Но одна и та же дорога может быть разной. Когда-то расстояния наносились на карту в днях пути, и путь туда мог не равняться пути обратно. Ведь есть существенная разница, плетешься ли ты в гору или весело переставляешь ноги, спускаясь с горы.
При принятии решений расстояния между объектами также можно мерить по-разному, в зависимости от того, какая перед нами стоит задача и с какими данными мы имеем дело. В этой статье мы рассмотрим несколько методов определения расстояния между объектами и путей применения их на практике.
При принятии решений нам часто необходимо сравнивать объекты между собой. Среди прочего можно использовать представление этих объектов как точек в некотором многомерном пространстве. Допустим нам необходимо выбрать офис для филиала компании.
Для начала определимся с критериями, по которым мы будем оценивать имеющиеся предложения. Пусть это будут расстояние от складов, стоимость аренды, размер помещений и то, насколько нам нравится данный офис (вложим сюда субъективную оценку инфраструктуры). Каждое предложение, таким образом, может быть представлено в виде точки в четырехмерном пространстве.
В обычной жизни мы привыкли к расстоянию, измеренному с помощью формулы Евклида, – корень из суммы квадратов расстояний по каждому измерению. То есть, если нам нужно померить расстояние между диагонально расположенными углами коробки, размеры которой нам известны, нам не обязательно искать линейку. Если под рукой есть калькулятор, достаточно сложить квадраты ширины, высоты и длины и вычислить из них корень. Обратите внимание, формула работает как на плоскости, так и на объеме. Более того, формула верна и для большего числа измерений. Но не во всякой ситуации.
Обратимся за примером к карте Манхеттена (Нью-Йорк). Его география чрезвычайно проста и сводится к формуле: с севера на юг идут авеню, с запада на восток – стрит (см. рис. 1). Если вам надо попасть от южного конца первого авеню к пересечению Мэдисон-авеню и 96-й стрит, вы вольны выбрать любой маршрут. Если при этом вы всегда будете двигаться в сторону конечной точки, последовательно увеличивая номера стрит и авеню, которые вы прошли, расстояние, которое вы пройдете, не будет зависеть от конкретного выбранного маршрута. Оно будет равно сумме расстояния, пройденного по стрит, и расстояния, пройденного по авеню. Или иными словами – сумме расстояний между точками по каждому из параметров.
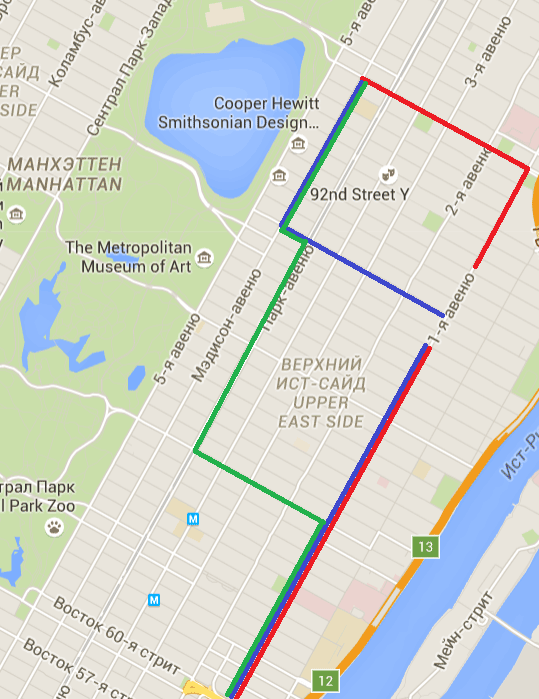
Рисунок 1. Манхеттенское расстояние не зависит от выбранного маршрута (maps.google.ru) D = ∑|x1,i - x2,i|, где x1,i и x2,i – i-я координата первого и второго объекта соответственно
Складывать напрямую выбранные параметры мы не можем. В связи с этим попытаемся оценить полезность офиса по каждому из параметрове.
Так как у нас имеется фиксированное множество предложений, мы можем найти минимальное и максимальное значение каждого из параметров. Теперь можно считать, что минимальное значение параметра соответствует нулевому значению полезности (или, в нашем случае, выигрыша в полезности), максимальное значение – единице, а все остальные значения находятся между нулем и единицей. За счет этого нехитрого трюка мы свели все параметры к одной безразмерной шкале, причем значения всех параметров измеряются от нуля до единицы. Теперь мы можем сравнивать тысячи рублей с единицами километров, и это не нарушит физический смысл задачи.
Но как нам сравнить офисы между собой? Очень просто, давайте сложим все значения полезностей для каждого из параметров. Количество параметров фиксировано, минимальное значение полезности равно нулю, максимальное – четырем. Отранжируем полученные значения и выберем тот офис, значение полезности у которого оказалось максимальным.
| Кстати
На самом деле формулы для евклидового расстояния, манхеттенского расстояния и расстояния Чебышева выводятся из метрики Минковского:
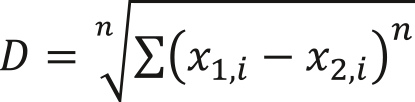
При n=1 получаем модуль разницы, то есть манхеттенское расстояние:
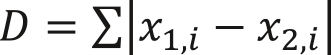
При n=2 получаем формулу Евклида:
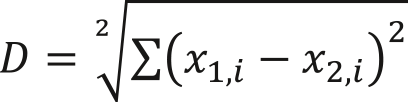
При n=∞ происходит следующее: самое большое значение параметра при возведении в бесконечную степень забивает остальные значения. Как следствие, после извлечения корня бесконечной степени мы получим только его, то есть просто самое большое значение:
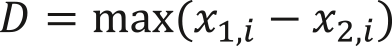
|
Поздравляю вас, вы использовали манхеттенское расстояние! В самом деле для того, чтобы определить разницу между офисами, мы используем разницу их полезности, определяемой как сумма разниц по каждому из параметров, то есть манхеттенское расстояние (еще известное как расстояние городских кварталов).
Но в отличие от Манхеттена Москва строилась не сразу, да и строилась по совсем другим принципам.
Допустим, что мы выбираем не офис, а квартиру. Для того чтобы оценить расстояние до работы мы будем использовать не километры, рассчитанные по формуле Евклида, а время, потраченное на дорогу. При этом? если у нас есть несколько вариантов маршрута, использующих различные виды транспорта, мы можем захотеть оценить это время по самому плохому варианту (надо же как-то объяснить риелтору, почему он должен дать нам скидку). В этом случае мы выберем максимум времени для путей на машине, трамвае и метро.
Такая оценка называется расстоянием Чебышева. В данном случае берется расстояние лишь по одному параметру, принимающему максимальное значение.
Мы могли бы использовать данную оценку и для выбора офиса. В этом случае будем смотреть не на сумму разницы полезностей по всем параметрам, а на максимум разницы между офисами.
Например, для двух офисов сумма полезностей примерно равна, но при этом инфраструктура первого офиса намного хуже инфраструктуры второго. Получается, что они не слишком отличаются по расстоянию, цене и площади, но очень отличаются по инфраструктуре. И захочется ли вам работать при прочих равных в плохих условиях? Нет, и в такой ситуации инфраструктура автоматически начинает иметь большее значение.
Теперь представим себе другую ситуацию. Пусть рассматриваемая система может иметь склонность к масштабированию. Например, если один город потребляет больше нашего товара, чем другой город, то это может попросту значить, что во втором городе больше жителей.
Впрочем, зависимость не всегда является столь очевидной. Для того чтобы бороться с подобной неоднозначностью, можно перейти к несколько иной логике измерения сходства между рассматриваемыми объектами. Перед этим мы считали каждый объект точкой в многомерном пространстве. Давайте представим теперь эту точку как один из концов вектора, причем все векторы будут стартовать в начале системы координат. Теперь вместо взаимного расположения точек и расстояний между ними мы можем использовать направление на объекты.
Представим себе, что перед нами экран радара, показывающего перемещения наших и чужих объектов: наши – с одной стороны, чужие – с другой. И те, и другие стараются перемещаться группами. В такой ситуации направление на объект становится более важным, чем расстояние до объекта.
Примерно так же направление становится более важным в пространстве с большим количеством признаков. Объекты, относящиеся к разным классам, обладают различными наборами признаков. Как следствие, для нас становится более важным, с какой стороны появились эти объекты, чем расстояние до них. Если количество параметров становится большим, само наличие или отсутствие значения по данному параметру может стать шумом.
В такой ситуации переходят к косинусной мере сходства. Не вдаваясь в подробности, определим ее как косинус угла между векторами, построенными на основе соответствующих объектов (см. рис. 2). Значения косинусной меры меняются от нуля до единицы.
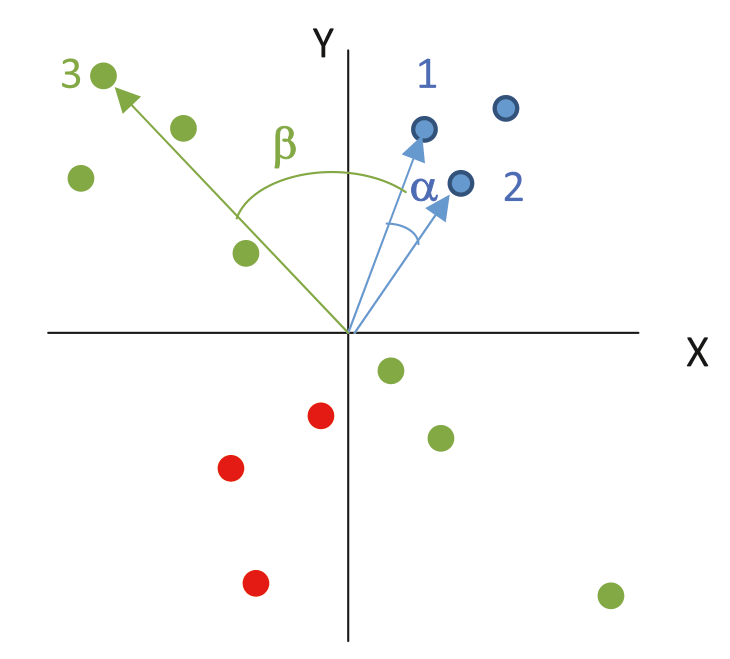
Рисунок 2. Расстояние между точками 1 и 2 равно cos(α), расстояние между точками 1 и 3 равно cos(β)
Если два объекта находятся на одной прямой, проходящей между началом координат, эти объекты считаются одинаковыми (расстояние равно нулю). Подобная ситуация соответствует уже описанному потреблению в городах: если потребление продуктов в первом городе во столько же раз больше, чем во втором, во сколько население первого превосходит население второго, то их векторы будут направлены по одной прямой.
На практике соотношение вряд ли будет выполняться очень точно, однако все объекты будут указывать в одну и ту же сторону. Если два объекта максимально непохожи друг на друга (их векторы перпендикулярны), расстояние между ними будет равно единице.
Пытливый читатель может возразить, что опытный исследователь быстро придет к тому, что вместо построения векторов в двумерном пространстве (потребление, размер населения) можно перейти к одному измерению (потребление на душу населения). Но что делать, если у нас имеются десятки тысяч параметров, а в числителе и знаменателе стоят не отдельные параметры, а их комбинации? Применение косинусной меры позволяет нам в такой ситуации положиться на то, что векторы сами укажут на подобное соотношение. Даже если на практике оно не имеет формально описываемого смысла.
Но приведенные рассуждения наталкивают нас на еще одну мысль. А что если вместо привычной декартовой системы координат (привычной карты, см. рис. 3А) нам перейти к полярной (экран радара, показывающий угол на цель и дистанцию до нее, см. рис. 3В)? Особенно удобна такая ситуация в случаях, когда свои находятся близко, а чужие далеко. Тогда вместо того, чтобы пытаться описать несколько областей на плоскости, мы можем сказать, что вне зависимости от угла все, кто расположен на расстоянии меньше заданного, – свои, а все остальные – чужие (причем чужих можно различать в зависимости от угла на них).
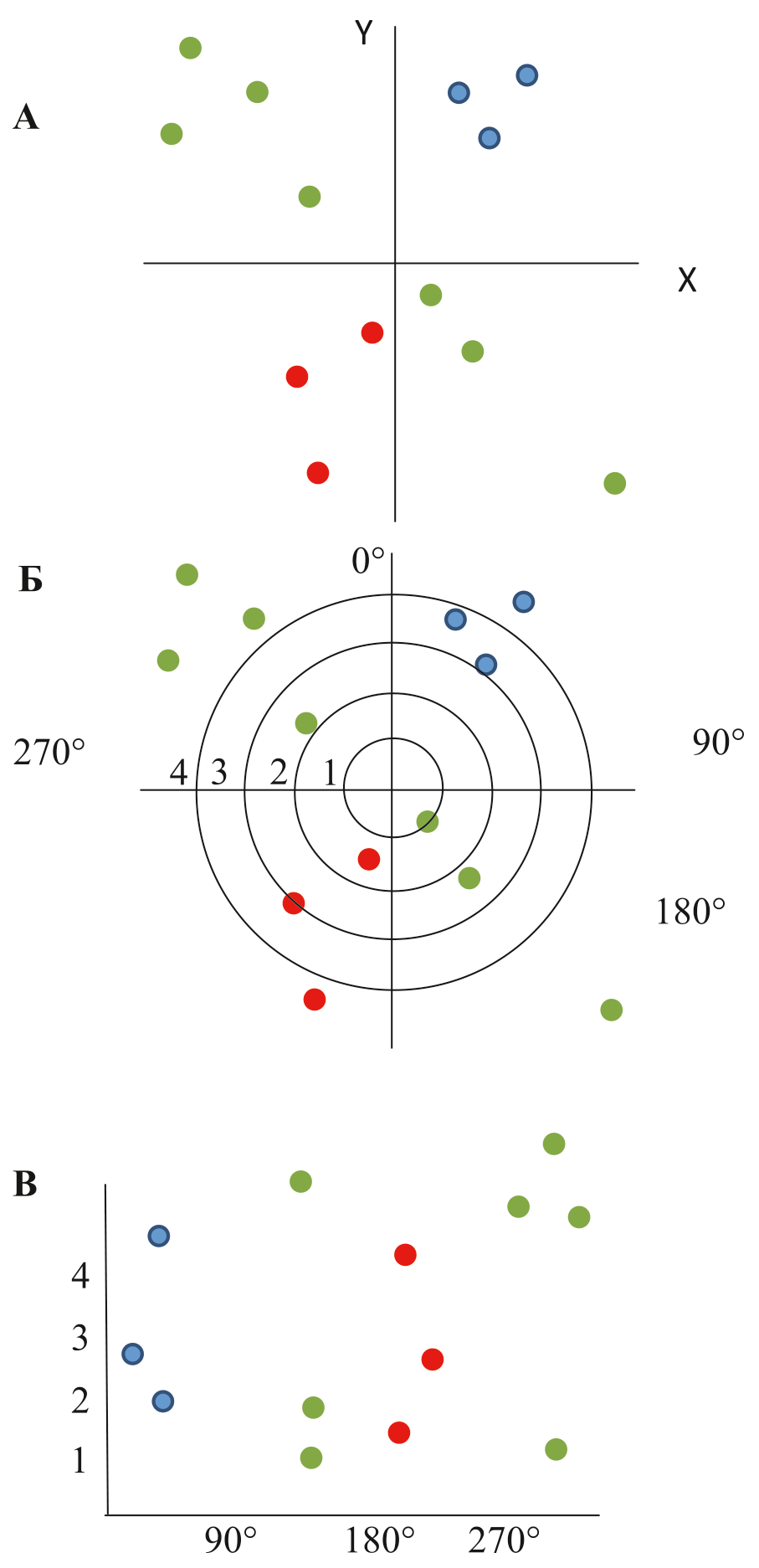
Рисунок 3. Переходя от А к Б, мы переводим декартову систему координат в полярную, а при переходе к В отображаем точки в новой системе
Хлопотная и сложная задача становится простой после некоторого трюка – преобразования системы координат. Подобные преобразования могут проводиться по-разному, но общий смысл их примерно одинаков – мы пытаемся посмотреть на пространство по-другому и поменять систему координат. Правда, не все преобразования так же очевидны, как полярная система координат, поэтому мы не будем их сейчас рассматривать, а перейдем к следующей мере, определяющей сходство объектов.
Одним из вариантов преобразования пространства является сокращение его размерности с помощью таких методов, как метод главных компонент, эластичные карты или t-SNE.
Данные методы позволяют выделить комбинацию из нескольких главных параметров (в случае метода главных компонент) и представить точки в этом новом пространстве. Или попытаться натянуть на точки гибкий коврик и посмотреть, как они там расположатся (в случае метода эластичных карт). Или попытаться «вжать» точки в плоскость (как поступает метод t-SNE). В этом новом пространстве расположение точек может оказаться более удобным, чем в исходном многомерном.
Иногда нам гораздо важнее, что координаты объектов ведут себя сходным образом. Часть параметров принимает относительно небольшие значения, часть, наоборот, стремится вверх. Подобное поведение описывается с помощью корреляции, вычисляемой на двух последовательностях чисел.
Корреляция принимает значения от –1 до +1. Значение +1 говорит о том, что одна последовательность полностью повторяет поведение другой. Так, например, стоимость офисов в одном районе обычно коррелирует с их площадью, то есть увеличение площади влечет за собой рост цены и наоборот.
Корреляция, равная –1, означает противоположное поведение (рост загрязненности воздуха приводит к падению цены). Корреляция, равная нулю, означает полную независимость параметров (светимость Алголя от фаз Луны).
Примеры различных функций и их корреляций приведены на рис. 4. На практике корреляция ниже 0,8 означают очень невысокую зависимость параметров. Существует несколько вариантов вычисления корреляции, но обычно используется формула Пирсона.
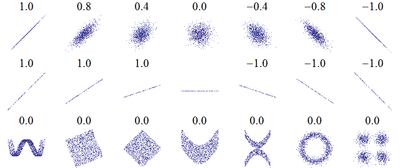
Рисунок 4. Значение корреляции для различных функций (изображение взято с сайта ru.wikipedia.org)
Если вернуться к нашему примеру с арендой офиса, то с помощью корреляции можно будет, например, выделить три группы офисов.
В первой расстояние до складов будет невысоким и цена офиса также будет невысока, то есть офисы будут расположены недалеко от складов на окраине города. В нее же войдут офисы, расположенные далеко от складов, и дорогие, то есть расположенные ближе к центру. Эти две группы объединятся, так как и там, и там цены и расстояние находятся на одном уровне полезности.
Вторую группу составят недорогие офисы, расположенные далеко от складов, то есть на другом конце города или еще дальше от центра, чем склады.
Наконец, в третью группу попадут склады, расположенные недалеко от офиса, но дорогие (арендаторы зачем-то решили поднять цены?). И если первая группа имеет для нас какую-то ценность, то зачем смотреть на последние две?
На практике все может пойти не так. Использование различных мер сходства подобно расстановке запятых в фразе «Садись в ногах правды нет». Запятые после первого и третьего слов имеют очень разный смысл и приводят к различным результатам. Но как говорится: «Любой бой, который мы выиграли, является честным». Нам ведь нужно принять правильное решение и обосновать его. Здесь любая мера определения расстояния может быть одинаково ценна, особенно если заранее неизвестно, какая из них правильная.
Перед нами есть карта, и мы меряем расстояния по ней. Но фактически надо смотреть на подписи к карте, говорящие, что путь туда не равен пути оттуда. Если бы у нас был тоннель, мы могли бы смело аппроксимировать ситуацию по формуле Евклида. Но на самом деле придется идти через горы и овраги, поэтому больше подойдет манхеттенское расстояние или расстояние Чебышева (потому что 100 метров вверх – это много больше, чем 100 метров вперед).
В данной статье мы не рассмотрели более экзотические, но от этого не менее полезные расстояния Махаланобиса, Хэмминга, Дайса и французских железных дорог. Но ведь нашей задачей не было вот так сразу раскрыть все секреты, правда? Нам нужно было узнать, что расстояния могут измеряться по-разному, в зависимости от того, какая нам попалась задача. бит
1 Автор все еще признателен Катерине Ляско за идею названия и аннотации данной статьи (см. «БИТ», №1, 2 и 3/2016).
2 Мы уже говорили о полезности в первой статье из данной серии («БИТ», №1/2016). В начало⇑
Facebook
Мой мир
Вконтакте
Одноклассники
Google+
Комментарии отсутствуют
Комментарии могут отставлять только зарегистрированные пользователи
|
Вакансии на сайте Jooble
|