Поиск по сайту

bit.samag.ru

Web

Рассылка Subscribe.ru

подписаться письмом

Вход в систему


Запомнить меня
Регистрация Забыли пароль?

О журнале

Ваше мнение

Статьи

Общие тенденции и тренды

Архив

Мероприятия

Календарь мероприятий

декабрь

2024

показать все

Новости партнеров

29.11.2024

Сайберус создает новую ИБ-компанию на основе технологий и экспертизы F.A.C.C.T.

29.11.2024

ГК InfoWatch представила новую версию InfoWatch ARMA Стена (NGFW) 4.4.

29.11.2024

ARinteg про архиватор ARZip: что изменилось в функционале и интерфейсе?

29.11.2024

Avanpost представляет бесплатную и промышленную версии службы каталогов Avanpost DS

29.11.2024

Новая версия «Блокхост-Сеть 4»: решение для импортозамещения

показать все

Статьи

22.11.2024

Тандем технологий – драйвер инноваций.

21.11.2024

ИИ: маршрут не построен, но уже проектируется

18.11.2024

Глеб Шкрябин: «Надежные и масштабируемые системы — основа стабильной работы бизнеса в условиях больших нагрузок»

14.10.2024

Елена Ситдикова: «На разработчиках программного обеспечения для транспорта лежит большая ответственность перед пассажирами»

13.06.2024

Взгляд в перспективу: что будет двигать отрасль информационной безопасности

18.04.2024

5 способов повысить безопасность электронной подписи

18.04.2024

Как искусственный интеллект изменит экономику

18.04.2024

Неочевидный САПР: выход ПО за рамки конструкторской деятельности

18.04.2024

Скоро некому будет делать сайты и заниматься версткой

показать все

Нечеткая логика. Как рекомендательная система повышает эффективность интернет-магазинов

Главная / Архив номеров / 2018 / Выпуск №07 (80) / Нечеткая логика. Как рекомендательная система повышает эффективность интернет-магазинов

Рубрика: Тема номера / Бизнес и экономика знаний

Сергей Амелькин, Денис Понизовкин, к.т.н., научный сотрудник, Финансовый университет; научный сотрудник, Институт программных систем имени А.К. Айламазяна РАН

Нечеткая логика
Как рекомендательная система повышает эффективность интернет-магазинов

С интенсивным развитием веб-технологий, огромным и постоянно растущим числом информации, доступной через интернет с помощью множества различных устройств, популярными становятся рекомендательные системы (далее РС), которые облегчают пользователю задачу поиска нужной информации путем рекомендации такой информации или путем определения степени близости конкретной информации (объекта) пользователю

Например, объектами могут быть товары, предлагаемые интернет-магазинами, а пользователи – это покупатели в этих интернет-магазинах. В случае когда товары могут быть определены набором свойств, например если товары представляют собой результаты интеллектуальной деятельности (например контент книг, художественных произведений, кинофильмов и пр.), возникает задача идентификации пользователей так, чтобы рекомендательная система определила те значения свойств, которые наиболее близки запросам пользователя.

Эффективность работы РС для интернет-магазинов определяется в большой степени эффектом длинного хвоста [1]: более 70% всех запросов производится потребителями нишевого контента (см. рис. 1). Это значит, что точность выбора рекомендаций имеет большое, прежде всего коммерческое, значение.

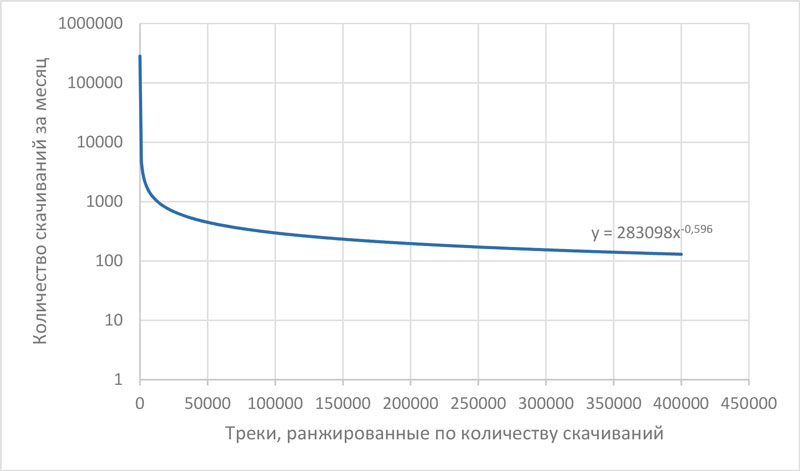
Рисунок 1. Эффективность работы РС для интернет-магазинов определяется в большой степени эффектом длинного хвоста

Для описания близости вводится функция оценки близости пользователей и объектов:

ρ: U × I → {[0, 1] ∪ ⊥}

Здесь U – множество пользователей РС, I – множество объектов, символ ⊥ означает неизвестное значение.

Для каждого пользователя u ∈ U = {1, ..., m} и каждого объекта i ∈ I = {1, ..., n} значение ρ(u, i) показывает, насколько объект i по своим характеристикам близок предпочтениям пользователя u.

Как правило, оценки близости задаются самими пользователями во время работы с РС. Будем считать, что чем меньше значение оценки, тем объект ближе.

Будем говорить, что между пользователем u и объектом i выполняется отношение близости R, если ρ(u, i) ≤ εR, где εR ∈ [0, 1] – некоторая малая фиксированная величина. Будем называть таких пользователей и объектов близкими.

Зачастую в исследованиях РС исходные данные представляются в виде матрицы, элементами которой являются значения ρ(u, i). Как правило, если ρ(u, i) ≠ ⊥, то это значение задал сам пользователь за время работы с системой (к примеру, поставил оценку фильму):

Матрица Mρ является разреженной, т.е. большинство значений ρ(u, i) = ⊥. Разреженность матрицы Mρ – это причина существования проблемы поиска нужной информации, иначе от системы требовалось бы только выбрать подмножества объектов с заданной оценкой близости.

Эта же причина послужила толчком для возникновения и развития РС как инструмента, способного снизить степень разреженности для каждого пользователя (называемого в таком случае активным и обозначаемого символом ua) путем решения следующих двух задач:

Прогнозирование (обозначим как pred). В данной задаче требуется спрогнозировать неизвестное значение ρ(ua, i⊥) для заданного и неоцененного объекта i⊥.
Выбор N наиболее близких к ua объектов: topN. В данной задаче требуется сформировать подмножество объектов ItopN = {i : (uaRi) ∧ ρ(ua, i) = ⊥} ∧ |ItopN | = N < n.

Существуют различные математические модели РС, которые задают способ представления данных о пользователях и объектах и методы решения задач. Рассмотрим одну из самых известных, хорошо изученных моделей РС – анамнестическую коллаборативную модель РС (далее АКМ).

Эффективность работы РС для интернет-магазинов определяется в большой степени эффектом длинного хвоста: более 70% всех запросов производится потребителями нишевого контента

АКМ является одним из классов моделей, применяющих методы коллаборативной фильтрации. Методы решений задач АКМ используют анамнестические алгоритмы, которые основаны на аксиомах, являющихся эвристическими утверждениями [2]. РС, использующие АКМ, внедрены во многих известных веб-сервисах: Amazon, Netflix, IMDB, Kinopoisk, LastFm и т.д.

Для того чтобы описать существующие проблемы, введем понятие эффективности модели. Будем говорить, что модель РС эффективна по некоторому критерию, если она удовлетворяет ему независимо от дополнительных условий и ограничений. Обычно [3] рассматриваются три критерия эффективности РС:

качество решения,
вычислительная сложность,
стабильность, где стабильностью будем называть свойство системы решать задачу качественно независимо от исходных данных.

Чтобы определить эффективность по критерию качества или стабильности, проводится тестирование. Для этого исходное множество данных P разбивается на обучающее и тестовое множества, которые обозначим символами P0 и P⊥ соответственно. Если (u, i, ρ(u, i)) ∈ P0, то будем обозначать такие объекты i0. Если (u, i, ρ(u, i)) ∈ P⊥, то будем обозначать такие объекты i⊥. После получения результирующего множества P⊥ = {(u, i, ρ(ua, i))} в ходе решения задачи по данным обучающего множества проводится сравнение результирующего множества с тестовым. Сравнение производится с помощью функций, называемых оценками качества.

Для каждой задачи существует своя группа оценок, в которую входит некоторое число функций. Например, некоторые из оценок задачи pred – это MAE, NMAE, RMSE [4], из оценок задачи topN – точность P, точность P@L по списку длины L, NDCG [4].

Будем говорить, что решение задачи t эффективно по критерию качества, если Et(P ⊥, P⊥) ≤ εt, где t ∈ {topN, pred}, Et – оценка качества решения задачи t, εt ∈ [0, 1] – некоторая фиксированная величина.

Как говорилось выше, АКМ основана на эвристических утверждениях. Выполнение эвристических утверждений в существующих исследованиях не рассматривается, но оно обусловлено свойствами исходных данных.

Если исходные данные обладают свойствами динамики или неоднородности, то эвристические утверждения не выполняются. Поскольку на них базируются методы решений задач, то нет гарантии получения эффективного решения по критерию качества на любых исходных данных или на одних и тех же данных, но меняющихся со временем. Поэтому коллаборативные модели не являются эффективными по критерию стабильности.

Реальные данные, как правило, обладают и тем, и другим свойствами. Зависимость качества решения от свойств исходных данных приводит к тому, что конкретная реализация РС эффективна по критерию качества на определенных данных или в определенный момент времени, но может быть неэффективной на других данных или в следующий момент времени. Поэтому существующие модели с течением времени требуют внесения доработок, а задача поиска универсальной модели, которую можно применять в различных предметных областях, актуальна для отрасли РС.

В нечеткой модели гарантируется выполнение необходимого условия эффективности решения

Обеспечить универсальность и эффективность коллаборативных моделей может использование нечетких множеств. Мы определяем контент как нечеткое множество, и это позволяет нам использовать такие операции над контентами, как их пересечение, объединение и дополнение.

Например, пересечение контентов пользователей u1 и u2, заданных на универсальном множестве характеристик X, – это наибольшее нечеткое множество cX(v) = cX(1u) ∪ cX(u2), содержащееся одновременно и в cX(u1), и в cX(u2), с функцией принадлежности wU, заданной следующей формулой:

cX(u1) ∩ cX(u2) = cX(v) : ∀x ∈ XwU(v, x) = min(wU(u1, x), wU(u2, x))

Аналогично задаются другие операции над контентами как пользователей, так и объектов.

С помощью аппарата теории нечетких множеств мы можем определить понятие близости для пользователей и объектов, как основных показателей, правильный расчет которых обеспечивает эффективную работу рекомендательных систем. В предлагаемой модели сопоставление информации о пользователе и объекте определяется заданием нечеткого отображения:

cδ : X × Y → [0,1]

именуемым сходством характеристик. Функция сходства cδ может быть задана в табличной или аналитической форме, а ее значения могут быть сформированы алгоритмически, к примеру помощью методов классификации, или экспертно, с помощью экспертных знаний о прикладной области РС.

С помощью функции cδ можно определить нечеткое отображение Ψ : X → Y контента пользователя на множество контентов объектов. Для этого зададим характеристическую функцию принадлежности νΨ характеристики к нечеткому подмножеству универсального множества Y при отображении Ψ следующей формулой:

νΨ(y) = max min{δc(x,y);wU(u, x)}

Определим функцию отображения контентов пользователей:

Ψ(cX(u)) = {(y|νΨ(y))}, y ∈ Y

При наличии способа отображения контента пользователя можно строго определить функцию близости ρ(u,i) между пользователем u и объектом i. Нечеткое правило алгоритмического вывода значения прогнозной функции близости нечеткой модели заключается в задании оценки сходства δc и в дальнейшем расчете прогнозной функции ρ.

Применение коллаборативных правил вывода в нечеткой модели описывается следующим образом. Разработанная нечеткая модель не является жесткой альтернативой, перечеркивающей применение коллаборативных правил вывода, допускается применение методов коллаборативной фильтрации, но предлагается использовать способ представления данных и отношения близости способами нечеткой модели.

При применении правила вывода не всегда получение эффективного решения по критерию качества зависит от меры сходства и порогового значения. Разработанная нечеткая модель позволяет применить правило вывода так, чтобы выполнялись достаточные и необходимые условия эффективности.

Нечеткая модель является эффективным расширением существующей анамнестической коллаборативной модели рекомендательной системы

Решение задачи topN при применении правила вывода заключается в формировании кластера Ni topN = {i : iRi0}. Необходимое условие точности решения заключается в выполнении свойства транзитивности отношения близости, что зависит от меры сходства и порогового значения. В нечеткой модели введена функция близости ρi, определим отношение iRi0 следующим образом:

iRi0 ⇔ ∃i0 ∈ I0 : ρi (i, i0) = 0

В нечеткой модели гарантируется выполнение необходимого условия эффективности решения. Выполнение условия эффективности решения достигается за счет метрических свойств используемой функции расстояния. Так как ∀i0 ∃i⊥ : i0Ri⊥, по построению решения в результирующее множество входят такие объекты i, что: ∃i0 : ρi(i0, i) = 0.

Но также ∃i⊥ : ρi (i0, i⊥) = 0. Так как функция ρi обладает метрическими свойствами, то ρi(i, i⊥) ≤ ρi(i0, i)+ρi(i0, i⊥) = 0, и потому iRi⊥. То есть выполняется необходимое свойство транзитивности: (iRi0) ∧ (i0Ri⊥) ⇒ iRi⊥.

Применение правила вывода в нечеткой модели более эффективно по критерию качества, чем применение того же правила в стандартных эвристических моделях. Это следует из того, что в нечеткой модели выполняется необходимое условие эффективности решения.

Значение оценок качества задачи topN зависит от числа K, зависящего от прогноза весовой функции s:

K = |I′| = |{i : (i ∈ ItopN ) ∧ (s(i) = 1)}|

Решение задачи topN эффективно по оценке качества, если K ≥ N (1 − εtopN). Покажем, что это верно для каждой оценки, на примере точности (а оценки качества одного класса коррелируют между собой):

i EtopN ≤ 1 – K N ≤ 1 − (1 − εtopN ) ≤ εtopN

Поскольку приведенные оценки зависят от величины K, будем рассматривать обобщенную целевую оценку качества решения задачи topN как функцию aEtopN (K) при применении весовой функции s и обобщенную объектно-ориентированную оценку iEtopN (K) при применении s.

Рассмотрим, какие условия влияют на эффективность решения задачи topN по критерию качества. При данном рассмотрении будем анализировать значения iEtopN, так как именно объектно-ориентированные (а не целевые) оценки качества применяются при тестировании рекомендательной модели. Рассмотрим необходимые и достаточные условия эффективности решения по критерию качества при применении правил вывода.

Необходимым условием эффективности решения задачи topN по критерию качества является выполнение транзитивности отношения близости объектов на множестве

I′ topN ∪ I a0 ∪ Ia ⊥,

где:

I′ topN ⊂ ItopN,

|I′ | = K ≥ N·(1−εtopN ): (i0 R i) ∧ (i0 R i⊥) ⇒ (i R i⊥),

i ∈ I′ topN

Покажем, что:

(iEtopN ≤ εtopN ) ⇒ ((i0 R i) ∧ (i0 R i⊥) ⇒ i R i⊥), i ∈ I′topN

Пусть (iEtopN ≤ εtopN) верно. Рассмотрим выражение:

(i0 R i) ∧ (i0 R i⊥) ⇒ i R i⊥,

а точнее, его левую часть (i0Ri) ∧ (i0Ri⊥).

По способу задания отношения близости между объектом, входящим в результирующее множество, и центром Ia0 кластера N i topN выполняется, что ∀ i ∈ ItopN ∃ i0 ∈ Ia0: i0Ri. Поэтому по построению решения верно, что i0Ri для всех i, i0 ∈ Ia0. Это означает, что выполняется i0Ri⊥.

Таким образом, левая часть решения выполняется по построению решения. Рассмотрим выполнение правой части выражения – iRi⊥.

Так как решение эффективно по критерию качества (то есть iEtopN ≤ εtopN), то ∃ I′topN ⊂ ItopN, I′ topN = {i : ∃ i⊥, iRi⊥}, |I′ topN | = K ≥ N · (1 − εtopN ). То есть выполняется правая часть выражения.

Таким образом, получаем, что если решение эффективно по критерию качества, то выполняется транзитивность отношения близости для i ∈ I′topN. Чем меньше число K, тем меньшее количество раз выполняется транзитивность отношения близости и тем решение хуже.

Таким образом, показано, что в об-щем случае анамнестическая коллаборативная модель не является эффективной моделью рекомендательной системы, а нечеткая модель является эффективным расширением существующей анамнестической коллаборативной модели.

C. Anderson The Long Tail: Why the Future of Business Is Selling Less of More. New York: Hyperion, 2006.
Aggrawal C. C. Recommender Systems. Springer, 2016.
Cleger-Tamayo S., Fernandez-Luna J. M., Huete J. F. A new criteria for selecting neighborhood in memory-based recommender systems // Proceedings of the 14th international conference on Advances in artificial intelligence. SAAI: 2011, pp. 423-432.
Ma H. Learning to recommend. The Chinese University of Hong Kong, 2009.

В начало⇑

Комментарии отсутствуют

Комментарии могут отставлять только зарегистрированные пользователи